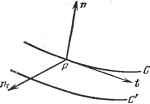Применим теорему Остроградского к вектору аХп: jdiv(aXn)dz= j (aXn)-da.

t S+S+X

Вектор da имеет длину da и отложен по нормали к поверхности. На поверхности 5 вектор da = nda. а на поверхности Е вектор da = nda (через j обозначается орт нормали к поверхности Е). Имеем

J div (а X п) dz= j {аХп) nda-{- j (а X п) щ da.

Смешанное произведение (аХп)- п, очевидно, равно нулю, так как векторы аХп и п ортогональны. Поэтому предыдущая формула принимает вид

di\{aXn)dz -(аХп)-iiyda.

Смешанное произведение (а X i = X i) а. Но пХ - это орт t касательной к кривой С при условии, что точка Р находится на этой

кривой С (рис. 3.17). Следовательно,

пХщ = (.

Далее, согласно формуле (28) и доказанному выше равенству rot п = О, находим

div (а X и) = rot а - а rot га = rot а. Таким образом,

/п - rot adz = \ а tda. J

Если расстояние PP = db мало, то dz = dado, где da -элемент поверхности 5. Если da - элемент поверхности - Е, то da = dldb, где dl - элемент кривой С. Тогда

db j п - roiada = db j а tdl = db j а dM,

s с с

откуда и получается формула Стокса

jn-rotada=. ja-dM. (52)

Итак, циркуляция вектора а по замкнутой кривой С равна потоку его вихря через поверхность, ограниченную С *). В случае соленоидального векторного поля а известно, что а является производной от вектор-

*) 1. Легко непосредственно убедиться в том, что в формуле (52) можно брать любую поверхность S, стягиваемую замкнутой кривой С. Действительно, пусть S, и - такие поверхности. Тогда поверхность S,+ ограничивает трехмерное тело с объемом т. Учитывая, что только для одной поверхности S, или 2 направление внешней нормали совпадает с положительным направлением нормали п, и применяя формулу Остроградского, получим

J п Tot а da -- j n-TOtada= j n rot a da = j div rot a = 0,

так как div rot a = 0.

2. Формула Стокса может быть обобщена аналогично формуле Остроградского (см. п. 3.3.2). Соответствующие формулы удобно получить из операторного соотношения (ср. сноску на стр. 140):

JdoXV= j dM, dj = nda, dM = tdl, (*)

ного потенциала 1), т. е. а = rot v. По формуле Стокса поток вектор-а rot V через поверхность равен циркуляции v по контуру, ограничивающему эту поверхность. Таким образом, поток соленоидального вектора через поверхность равен циркуляции его векторного потенциала по контуру этой поверхности.

Теорема Стокса позволяет дать новое определение вихря. Для этого определим составляющую rot а в точке А по любому фиксированному направлению AW.

Опишем из точки А, как из центра, окружность С малого радиуса г, лежащую в плоскости, перпендикулярной рассматриваемому направлению (рис. 3.18). Составляющая вихря по направлению AW имеет следующий вид:

а - dl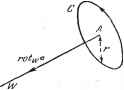

rotvT а !im -

r->0

dl=tdl = dM.

(53)

Рис. 3.18.

Приложение векторного исчисления к теории электромагнитного поля

3.3.10, Электростатическое поле. Рассмотрим два точечных заряда Qj и Qs- помещенных в пустоте в точках А к В на расстоянии г друг от друга (рис. 3.19). Тогда сила, действующая на заряд Qj, равна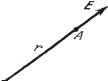

Рис. 3.19.

Рис. 3.20.

QjJ (закон Кулона),

где и - орт вектора В А. Пусть в точке О помещен заряд Q. Электрическое поле заряда Q в точке А равно силе, действующей на единичный заряд, помещенный в точке А (рис. 3.20):

4л8о г->-

Это электрическое поле представляет собой поле векторов, проходящих через фиксированную точку О. Используем формулы (40) и (41) для f(r) - Q 1

Имеем

4леп

div £ = 0,

где поверхность S ограничена замкнутым контуром С, причем направления п а t - ортов нормали к S и касательно!} к С - согласованы, как указано в начале настоящего пункта. В частности, формула (52) получается в результате скалярного умножения обеих чаете}} (*) на вектор а. Формула Стокса, строго говоря, верна только для поверхностно односвкзных областей (см. [2], стр. 305).

) Ниже все формулы даны в рационализированной системе единиц МКС, включающей четыре основные единицы: метр, килограмм-массу, секунду и ампер или вольт. В электротехнике для получения уравнений с наиболее простыми и симметричными размерностями часто берут за основные метр, секунду, вольт и ампер. Главные производные единицы; кулоьг; о.м, фарада, генри и т. д. Единицы, входящие в формулы, которыми мы пользуемся, это; единицы силы - ньютон (10* дин), единица напряженности электрического поля - вольт на метр, единица электростатической индукции - кулон на квадратный метр, единица электромагнитной индукции - вебер (10* гауссов) на квадратный метр. Рационализация вводит множитель /4 в оба основных закона Кулона (в электростатике и магнитостатике). Поэтому значения для диэлектрической и магнитной проницаемости в пустоте следующие;

= 10-3 (зб )-1 = 8,842 10->2 фарад на метр, Р-о = 4тс 10 = 1,257 10- генри на метр, причем еор.оС2 = 1, где скорость света с = 3-10* м/сек.

Если внутри поверхности 5 содержится несколько точечных зарядов Qi.....Qn- то

S 1 = 1

Предположим, что заряды распределены непрерывно внутри объема v и плотность распределения зарядов дается скалярной функцией точки р. Тогда соотношение div£=0 нарушается. Распространяя на этот случай теорему Гаусса, получим

/£..5=±/р<

а так как

J E-dS J div £

TO при непрерывном распределении зарядов

Далее, и поэтому

div£ = -P-.

div £ = -div grad 1 = - Д1, Д1/ i =: О (уравнение Пуассона).

До, сих пор мы рассматривали поле в пустоте. Обратимся теперь к полю внутри диэлектрика. В этом случае молекулы тела ведут себя как электрические диполи - каждый элемент объема содержит большое число зарядов противоположного знака, соединенных попарно.

При отсутствии внешнего поля моменты молекул ориентированы по-разному, и их векторная сумма равна нулю. При наличии внешнего поля диполи частично повернутся, и сумма моментов станет отличной от нуля.-Диэлектрик с ориентированными в той или иной степени дипольными моментами окажется поляризованным. Степень поляризации характеризуется

а скалярный потенциал Е равен

Применяя формулу (49) к замкнутой поверхности, не содержащей внутри себя точки О (теорема Остроградского, вообще говоря, неверна, если в области тройного интегрирования векторная функция имеет бесконечный разрыв), получим, что поток вектора Е через эту поверхность равен нулю. С другой стороны, непосредственно очевидно, что поток вектора Е через поверхность любого шара с центром в О равен Q/sq. Обозначим через 5 произвольную замкнутую поверхность, содержащую внутри себя точку .0 и проведем сферу с центром О, целиком находящуюся внутри 5. Применяя формулу (49) к области, ограниченной 5 и поверхностью этой сферы (учтем, что внутренняя нормаль сферы является внешней . для рассматриваемой области), получим

Г £ dS = - (теорема Гаусса).