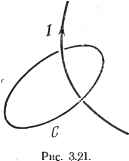*) Точнее, векторная функция точки Р определяется как производная от. суммарного момента молекул по трехмерной области ([2], стр. 311-312).

вектором поляризации Р, который, по определению, равен суммарному моменту молекул, отнесенному к единице объема *). Учет поляризации можно осуществить, если ввести фиктивную плотность электрических зарядов, равную - div Р. При этом условии теорема Гаусса записывается в следующей форме:

jЕ dS = j pdv- juiv Pdv.

S V V

Применяя формулу (49), получаем

j{e + P)-dS= fpdv.

В данном случае векторное поле, удовлетворяющее теореме Гаусса, имеет вид

D = eE + P.

Вектор D называется вектором электростатической индукции. Он, очевидно, удовлетворяет уравнению

divZ> = p.

3.3.11. Магнитное поле постоянных токов. Все, что говорилось выше относительно электрического поля Е, можно повторить для магнитного поля Н. Однако следует учитывать, что свободные магнитные заряды не существуют, т. е. вне магнитной среды

divЯ = 0.

Внутри магнитной среды присутствуют элементарные магниты. Повторяя предыдущие рассуждения, мы приходим к необходимости определить вектор магнитной индукции В, дивергецдия которого равна нулю как внутри, так и вне магнитной среды:

divB = 0.

Рассмотрим контур С, окружающий ток / (рис. 3.21). Циркуляция вектора магнитного поля по контуру С равна

j Н dl- / (теорема Ампера), с

Если внутри контура С тока нет, то

fHdl=0.

Из определения вихря по формуле (53) следует, что в точках, где тек отсутствует,

fH.dl

TOtwH== !im ---= 0 (IF -любое), т. е. го1Я=0.

3.3.12. Электромагнитное поле. Выпишем формулы, используемые при выводе уравнений Максвелла (см. 3.3.15):

div.S=0, (54)

div D = p, (55)

JH.dl=I. (56)

3.3.13. Закон Фарадея. Электродвижущая сила, индуктированная на контуре С, помещенном в электрическом поле Е, выражается криволинейным интегралом

fE.dL

Если обозначить через 5 какую-либо поверхность, опирающуюся на контур С (рис. 3.22), то согласно теореме Стокса получим

JEdl J rot E-dS.

-------\ По закону Фарадея индуктированная электродви-

Л жущая сила пропорциональна изменению потока В во времени, т. е.

РИС. 3.22. . frotE.dS = ~f.dS. .

В силу произвольности поверхности 5

3.3.14. Закон Ампера. Обозначим через J вектор плотности тока в точке. Тогда закон Ампера можно записать в виде

fHdl= fj-dS, (57)

так как поток вектора J через поверхность 5 равен интенсивности тока, проходящего по контуру С. В силу теоремы Стокса

f Н dl: fiotH dS. с s

Сравнивая с формулой (57), получим

rot H = J. . .(58)

Ток J создается зарядами, движущимися со скоростью V. Обозначим через р пространственную плотность этих зарядов. Очевидно, что вектор плотности тока

При этом формула (58) принимает вид

.rotH=pV. (59)

Возьмем дивергенцию от обеих частей этого равенства. Учитывая формулу (30), имеем

div(pyj = 0. . (60)

dt df

Используя две последние формулы, получим

div(pV)= -div-.(61)

Формулы (60) и (61) противоречивы.

3.3.! 5. Уравнения Максвелла. Чтобы устранить полученное противоречие. Максвелл видоизменил закон Ампера следующим образом: полный ток, который мы рассматриваем, состоит не только из тока проводимости pV, но

и из тока смещения Поэтому вектор J=pV следует заменить на

1/1 dD

и тогда уравнение Ампера (59) примет вид

го1Я=рУ + 4.

Таким образом, получаем систему уравнений Максвелла:

div D =: р, uiv В = 0,

wtE=--, . (62)

rot H = J + .

Для пустоты система уравнений Максвелла (62) переписывается в виде

div£ = 0, divW = 0.

rot£ = -p-o. (63)

rot Я:

0 dt

3.3.16. Векторный потенциал магнитного поля, возбужденного током.

Рассмотрим электрический заряд е, перемещающийся со скоростью V. Он эквивалентен электрическому току силы /, текущему по элементу длины dl:

Idl=eV. (64)

Величина /. положительна, если направление тока совпадает с направлением вектора dl.

Магнитное поле, создаваемое рассматриваемым движущимся зарядом на расстоянии г от этого заряда, равно (формула Био - Савара - Лапласа)

Формула (51) дает

div(pV) = ---. Дифференцируем по времени равенство (55):