Так как divB -О, то для вектора В существует векторный потенциал А. Определим его. Имеем

В = rot Л.

В пустоте

В = ,Н,

поэтому

4я гЗ

(66)

Преобразуем формулу (66):

rot Л =

eVXi-+eVXJ + eVXk

) + JX

*x(-)j

+ УХ

Сравнивая полученную формулу с формулой (22), найдем, что

Применим полученную формулу для случая тока, текущего по проводу. Это важный частный случай движения заряженных частиц. Пусть dS - элемент поверхности, через который проходит ток /, J-вектор плотности тока.

Имеем JdS-I. Используя формулы (64) и (65), получим выражение для векторного потенциала тока в проводе А через интеграл, распространенный на объем V {dv == dS dz) рассматриваемого провода:

H(sy,

(67)

Рис. 3.23.

Применение этой формулы к электрической цепи, по которой идет ток, может привести к некоторым затруднениям. Рассмотрим, например, случай бесконечного прямолинейного провода. Пусть его сечение dS, а сила тока в нем /. Выделим мысленно отрезок АВ и найдем векторный потенциал, созданный током, текущим по этому отрезку. Рассмотрим точку Р, отстоящую от АВ на расстоянии d (рис. 3.23). Так как векторный потенциал обладает осевой симметрией относительно АВ, то при определении точки Р достаточно указать абсциссу точки Н и расстояние HP-d.

Пусть М - любая точка отрезка АВ, а Zy, z s п z - абсциссы точек А, В, Н, М относительно фиксированной точки О. Обозначим через г расстояние MP. Имеем Jdv - JdSdz - ldz. Поэтому формула (67) дает следующее выражение для векторного потенциала А:

21. 1

=1{ы \Mar-\-{z-sf iz -.)] i:::;,

а так как

Yd- + iZy-sf + z.-s

Yd + {z,-sY~(z,-s)

+ 1п [Yd--(Zi~sf -(2,~s)]}. (68>

Для перехода к бесконечному прямолинейному току нужно устремить 2j и 2 соответственно к -оо и -f-oo. При этом векторный потенциал также стремится к бесконечности.

Следует заметить, однако, что магнитное поле В рассматриваемого тока конечно. Поэтому должны быть конечны частные производные векторного потенциала А, так как

B = tot А.

Положим в формуле (68) d = d и s = s., и полученную постоянную-величину вычтем из правой части этой-формулы. Имеем с точностью до потенциала в фиксированной точке:

А =-/

I

{YA + (2 - S,f Ч- 2 - l) {VA + (i - Syf - {Z, ~ S,)) I

Если теперь устремить z и z соответственно к -оо и +оо, то

= i(ln-L ln-l 471 I d d\ j

Так как векторный потенциал определяется лишь с точностью до градиента скалярной функции (см. п. 3.2.18), то можно написать

д = Ё/(-1пй2).

Рис. 3.24.

Векторный потенциал тока в проводнике с любым поперечным сечением (рис. 3.24) выражается через поверхностный интеграл:

ddS.

3.4. СИСТЕМЫ ОРТОГОНАЛЬНЫХ КРИВОЛИНЕЙНЫХ КООРДИНАТ

3.4.1. Определение. Рассмотрим трехмерное пространство, в котором введена система прямоугольных координат Ох, Оу, Oz. Мы можем связать-это пространство с системой криволинейных координат. Пусть между прямоугольными координатами х, у, г и криволинейными координатами и, v. w устанавливается взаимно однозначное соответствие, описываемое формулами

х = р(и, V, w), y - q(u, V, w), z = r(u, v, w) (70)-

u=P( x, y, z) vQ{x, y, z), wRix, y, z). (71>

Уравнения и - const, v ~ const, w - const представляют собой уравнения координатных поверхностей криволинейной системы в прямоугольной системе координат.

Каждая пара координатных поверхностей, проходящих через фиксированную точку М, образует в пересечении координатную линию. Параметрические уравнения координатных линий получаются из уравнений (70), если в них поочередно изменять только одну из переменных и, V, w, оставляя при этом неизменными остальные две (рис. 3.25).

В этой главе мы ограничимся рассмотрением ортогональных криволинейных координат, неортогональные системы будут изучены в п. 5.2.1 и последующих. По определению, криволинейные координаты называются ортогональными, если в любой точке М касательные к координатным линиям образуют прямоугольный трехгранник.

Квадрат элемента длины ds в прямоугольных координатах дается формулой

ds = dx-\~df-\-dz-

В случае ортогональных криволинейных координат эта формула приобретает следующий вид: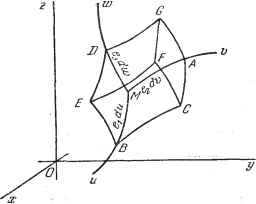

Рис. 3.25.

-где el, el

е\ обозначают величины

[ди] ~{ди) \ dm / V dm ) \ dm j

\ du

Если элемент ds параллелен касательной в точке М к оси Ми, то его длина будет равна е du. Аналогично длины элементов, параллельных осям Mv и Mw, равны 62dv и edw. Так как величины е, являются функ-

циями координат точки, их называют единицами локальной длины **).

Рассмотрим скалярную функцию точки V {х, у, z). Выражение этой функции в криволинейной системе координат получается простой заменой X, у, Z их значениями (70). Пусть теперь Л(х, у, z) - векторная функция точки, Л, Ау, А - проекции вектора Л на оси прямоугольной системы

*) Нетрудно показать, что необходимым и достаточным условием ортогональности системы криволинейных координат является условие, состоящее в том, чтобы выражение ds содержало только члены с квадратами дифференциалов (см., например, [3], стр. 340, 341).

**) Величины е 2, бз называются такжекоэффициентами Ламе, метрическими коэффициентами, масштабными множителями.