на площадь поверхности MAGD, т. е.

(MJ-( 24JJ. (76)

С помощью круговой перестановки цифр 1, 2, 3 и букв и, v, w, находим:

rot, А = -г4- Г- (еИи) - (езщ)

Отметим, что проекции Л , А, А можно определить по формулам (72) и (73).

Положим в (75) Л = grad К. Имеем

д ( евз dV

ди \ ди

езвх dV

\ 2 dv

/6,2 dV

Важнейшие системы ортогональных криволинейных координат

в пространстве

Рассмотрим несколько конкретных систем ортогональных координат. Эти системы будут использованы в гл. Vi при изучении уравнений распространения волн и Лапласа. С целью облегчения дальнейших вычислений мы приведем выражения для дивергенции, лапласиана, проекций градиента и вихря во всех рассмотренных ниже системах координат. Будем считать, что V и Л - соответственно скалярная и векторная функции точки.

3.4.3. Система цилиндрических координат. Координатные поверхности: круговые цилиндры с осью вращения Oz, плоскости, перпендикулярные оси Oz, и полуплоскости, проходящие через Oz (рис. 3.27). Цилиндрические координаты р, <р, Z связаны с прямоугольными координатами х, у, z соотношениями

x = pcoscp, y = psincp, z = z.

Уравнения координатных поверхностей соответственно в прямоугольной и цилиндрической системах имеют вид:

Рис. 3.27.

д;2 у2 р2 Р= const,

у/х = tg ф, ср = const, Z = const, z = const.

Квадрат элемента длины равен

ds = df + р2 dcf2 + dz, следовательно, единицы локальной длины равны

е, = 1, е = р.

*) Более детальный вывод формул этого пункта см., HanpH.viep, в [5J.

Согласно формулам п. 3.4.2 получаем:

dp div Л =

л dV

1 <5Л,

grad V = дА,

дУ dz

1 dA rot Л = -

го(Л = -

1 d 1 dA,

го1,Л = -Л-Н-р--y-:

ду- I dV . dV . 1 dV , dl/

dp I dp2

p2 ,j2

3.4.4. Система сферических координат. Координатные поверхности:: сферы с центром О и радиусом р, круговые конусы с вершиной О, образующие которых составляют с осью вращения Oz угол 6, и полуплоскости проходящие через Oz под углом <р к плоскости xOz (рис. 3.28).

Сферические координаты ) р, б, ср связаны с координатами х, у, z соотношениями

X = р sin 6 cos ср, у = psin 6 sincp, г = рсозе.

Уравнения координатных поверхностей соответственно в прямоугольной и сферической системах имеют вид:

х2-[-у2 2 р20, р = const,

x2 + y2 2:2tg2e4-0, 6 = const.

itgcp.

tp = const.

Квадрат элемента длины равен

ds = df И- p2dS2-(- p2 sin2 e d<p2,

следовательно, единицы локальной длины равны

ej=l, = р, £3 = psin 6. Согласно формулам п. 3.4.2 получаем: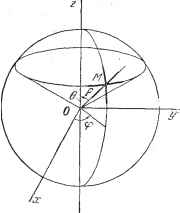

grad l/ = -, grad,V

divi4 =- Л

Р Р

ptge

го1 Л =

} dV р dO

I dA.

gradl/: 1 dЛв

Рис. 3.28.

1 дУ

а Sin 6 dc3

1 di

ptge

rotr, A = -

p sin e dy

Д1/ =

2 dV

) sin 6 dy

rotA = y Ло + , dV , 1

dO 1

--Л

psin6 dy d

p dp I dp2

ptge

psine dy2

) Координаты f и e часто называются долготой и дополнением широты (зенитным расстоянием).

3.4.5. Система параболических цилиндрических координат. Рассмотрим рис. 3.29, на котором представлены параболы двух семейств взаимно ортогональных софокусных парабол (фокус в начале координат). Проведем ось 0Z, перпендикулярную к плоскости OXY, и будем параллельно перемещать параболы при условии, что их фокусы остаются на оси 0Z. Тогда параболы обоих семейств опишут параболические цилиндры, образующие две системы взаимно ортогональных координатных поверхностей. Третья

система координатных поверхностей состоит из плоскостей, параллельных OXY. Если принять за оси прямоугольной системы координат Ох, Оу, Oz соответственно ОХ, 0Y, 0Z, то уравнения координатных поверхностей в прямоугольной и параболической цилиндрической системах имеют вид: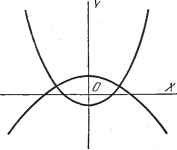

Рис. 3.29.

Z = const.

а= const,

Р = const, Z -- const.

Координаты а, р, z связаны с прямоугольными координатами соотно-.шениями:

X = cap, у = у (р2 - а), z = z. Квадрат элемента длины равен

= С2 (а2 + р2) (Йа2-(-dp2) £2,

Следовательно, единицы локальной длины равны

e, = , = c(a2+p2)V..

Для упрощения записи положим (а2--2)/ § Согласно формулам ;п. 3.4.2 получаем:

1 1 /<5Л

ШуЛ(аЛ +И,)+7(--+

grad,l/ = ;

1 дЛ дА

~сЪ ~Щ

1 дЛ

дА

°Ч--дГ~ сВ да 1 1 fdA,

rot - (аА - Иа) + -W {-д -

- сЧ \ до. д ) + dz

дА д

3.4.6. Система параболических координат вращения (параболоидальные координаты). При вращении фигуры на рис. 3.29 вокруг оси 0Y параболы обоих семейств опишут ортогональные параболоиды вращения, образующие две системы взаимно ортогональных координатных поверхностей. Третья -система координатных поверхностей состоит из полуплоскостей, проходящих через ось вращения. Если принять за оси прямоугольной системы коорди-