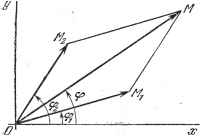функций, частоты которых сплошь заполняют числовую ось от нуля до бесконечности:

со со

f{t)z= I dia j f(z)cosw{t - x)dx.

о -co

Если, как в предыдущем случае, мы хотим изучить поведение электрической цепи с током i = f(t), то мы снова приходим к рассмотрению постоянных синусоидальных режимов. Из этого видна важность синусоидальных функций времени и интерес, который может представить разработка способов расчета, специально приспособленных для этих функций.

1.2.2. Графическое изображение синусоидальной функции. Рассмотрим вектор постоянной длины / вращающийся в заданной плоскости вокруг точки О с угловой скоростью со. Введем в указанной плоскости систему

прямоугольных координат хОу (рис. 1.9). Пусть 9,-угол, образованный ОЖ, с осью Ох в начальный момент времени. Тогда г, - ордината точки Ж, в момент времени t - выражается формулой

г, = /j sin (oit -f- (fj).

Вектор OAJj удобно использовать для графического представления синусоидальных функций ч времени (синус получится при проектировании на ось Оу, косинус - на ось Ох).

Пусть нам нужно сложить две синусоидальные функции с одинаковым -периодом, но с разными начальными фазами

г, = /, sin (oit -т- (pi), 2 = /g sin (ш --

По известному правилу вектор ОМ, изображающий сумму обеих функций и /g- можно получить как геометрическую сумму векторов ОМ и ОМ2, изображающих эти функции. Все три вектора вращаются одновременно с угловой скоростью tu. Легко непосредственно проверить, что ордината точки М представляет собой сумму функций /j sin(tu--cp,) и sin (со/--92)-.Аналогично абсцисса точки М равна сумме функций /, cos(to/--(f),) и /2 cos {Uit -j- 92)-

Вместо того чтобы вращать векторы с угловой скоростью со, можно -предположить, что они неподвижны, а оси координат вращаются с угловой скоростью - св.

На рис. 1.9 изображено относительное расположение векторов и осей (в момент / = 0).

Геометрическое построение, описанное выше, определяет амплитуду 0М = 1 и фазу 9 и тем самым позволяет найти выражения

/sin (tot--ср) = sin (со/-[-cpi)/2sin (св/-[-ср2), / cos (со/ -[- (р) = /, cos (св/ -\- (pi) -f- /2 cos (со/ -[- срг).

Часто нужно уметь вычислять производные или интегралы синусоидаль-.ных функций типа / = /sin(co/-f-(p). Имеем

Рис. 1.9.

= co/cos(cb/--(p)r= co/sin со/--ср-[-Y .

св/--ср- 2

idt =--- cos (со/ -j- (р) =: - sin

) Иногда функцию Ае- называют сиссоидалытой и обозначают А cis ф. Слог cis является сокращением от cosinus sinus. Здесь буква j заменена буквой i, как это принято в математике.

Производные и первообразные от функции t изображаются векторами, повернутыми по отношению к исходному вектору соответственно на угол

и -. Длины этих векторов будут ю/ и си. Такой прием позволяет графически получить синусоидальные решения дифференциальных или интегро-дифференциальных уравнений с постоянными коэффициентами.

Рассмотренный нами способ векторного представления весьма употребителен. Однако графические построения становятся неудобными и мало точными в случае длинных и сложных вычислений, особенно когда порядок величин векторов си/, /, си весьма различен. Способ же, который мы сейчас изложим, соединяет в себе простоту графического приема с точностью алгебраических вычислений.

1.2.3. Представление с помощью комплексных чисел. Поскольку речь идет о векторах, расположенных в одной плоскости, то можно плоскость на рис. 1.9 считать комплексной и трактовать вектор как комплексное число, вещественная и мнимая части которого представляют собой соответственно проекции вектора на оси Ох и Оу. Вектор ОМ определяется комплексным числом)

/ [cos (cuf + ср) + / sin (cu Н- ср)] = le-e .

Член =Ie определяет собой неподвижный вектор ОМ, отнесенный к неподвижным осям (рис. 1.9). Величина g называется комплексной амплитудой или просто комплексным током. Точно так же, рассматривая напряжение и = t/sin(cuf-)-6), мы можем ввести величину l/ = Ue, которую будем называть комплексным напряжением.

Покажем теперь, что сложение двух синусоидальных функций, изображенное на рис. 1.9, можно произвести и без графического построения. Действительно, пусть даны две (и-аи несколько) синусоидальных функций, представляющих собой, например, ток

г, = /, sin {(at + (pi), 2 = /2 sin (mt + cpj)-

Положим, что

Так как слож&ие комплексных чисел подчиняется правилу векторного сложения, то очевидно, что вектор ОМ на рис. 1.9 определяется комплексным числом = 1+2- Искомая синусоидальная функция будет представлять собой мнимую часть от е .

Производная по времени функции / = /sin(cuf-]-(p) будет мнимой частью производной по времени от функции е \ В этом легко убедиться непосредственно, если сравнить оба выражения. Точно так. же неопределенный интеграл по времени от i совпадает с мнимой частью интеграла от де . Отсюда можно вывести следующее правило: дано

jj = /j sin {iut -К ср,), J2 = 12 sin -I- 92) -

несколько синусоидальных функций. Требуется определить синусоидальную функцию, представляющую результат подстановки г i, ... в линейное и

*) Напомним, что в цепи переменного тока различают мгновенную мощность р, активную мощность (среднее за период значение мгновенной мощности) Р и так называемую реактивную мощность Q.

Если мы обозначим соответственно мгновенные значения тока и напряжения через г (О и (/). амплитуды этих величин через / и [/, а сдвиг фаз между ними через ¥, то упомянутые выше мощности определяются формулами: р = ijif) и (t), Р=/) = /{/cos Q = /(/Sin f.

однородное выражение первого порядка

... +Pi-§ + ?2 4t+ +-1/hdt+f hdt+ - (3) Здесь коэффициенты a, p, -jf не зависят от времени. Положим

Член е- входит множителем во все слагаемые выражения (3). Окончательный результат,очевидно, может быть написан в виде

Мнимая часть этого выражения и есть искомая синусоидальная функция

i = /sin(u)/ 4-9)-

Вешественная часть дает результат подстановки в (3) соответствующих косинусоидальных функций.

1.2,4. Ограничения метода. Только что установленное правило применимо в тех случаях, когда требуется произвести сложение, дифференцирование, интегрирование токов или синусоидальных напряжений либо линейные комбинации этих операций. Правило это, однако, неприменимо, если нужно подвергнуть токи или напряжения нелинейным алгебраическим операциям, как, например, умножению или возведению в степень. Действительно, легко видеть, что при таких операциях возникают круговые частоты, отличные от т. Это обрекает на неудачу векторное построение, изображенное на рис. 1.9, а следовательно, и комплексное представление, которое является его отображением.

Рассмотрим это на примере умножения. Пусть

i,= g,e-\ i,=ff2e-. g.h - c2-V-Правило умножения комплексных чисел, примененное к /,12. дает

; ,- -II J pi+-f2)-i-2yiot

Мнимая часть этого выражения равна

12 sii ( Pi -Ь ?2 + 2lSlt).

Если же непосредственно умножить /j -/jsin(ш/-l-cpi) на i - Is\n((sit то получим

hh - fhin (( t -I- 9,) sin (со/ -f (p) = i /,/2 [cos (91 - 92) - cos (2co/ 91 + 92)].

Результаты, как видим, получились совершенно различные.

Замечание. Комплексное исчисление может оказаться весьма полезным в тех случаях, когда требуется определить активную и реактивную мощности в цепи переменного тока *).