ГЛАВА IV МАТРИЧНОЕ ИСЧИСЛЕНИЕ

4.1. АЛГЕБРА МАТРИЦ

4.1.1. Плоское преобразование, понятие оператора. Обозначим через а операцию, преобразующую вектор и в другой вектор ©. Это преобразование можно символически написать в виде

аи==ю.

Если операция а преобразует каждый вектор в строго определенный вектор, то рассматриваемое преобразование однозначно.

Если операция а преобразует различные векторы в различные, т. е. неравенство ифю влечет за собой аи Ф аю, то она называется неособенной.

Если

а (си) = с (аи),

а (и --f- V) = au-\- ao,

где с - произвольная постоянная, а и о - произвольные векторы, то преобразование называется линейным. Ниже мы ограничимся только линейными операциями.

Принято называть а оператором преобразования.

Если вектор и, отличный от нуля, преобразуется в вектор о, имеющий то же направление, т. е. если преобразование а изменяет только длину или, как принято говорить, модуль вектора и, то, обозначив через X коэффициент

растяжения или сжатия длины вектора, получаем

аи = Хк.

(В этом равенстве а - оператор., а X-алгебраическое число.) Принято говорить, что направление вектора и - это собственное направление оператора а, а X - это соответствующее собственное значение.

Пример 1. Даны две взаимно перпендикулярные прямые OA, ОВ и вектор п. Пусть новый вектор V определяется следующим образом: его проекция на OA в 5 раз больще проекции а на OA, а его проекция на ОВ равна половине проекции и на ОВ (рис. 4.1).

Ясно, что если вектор а находится на прямой OA, то

аи = 5и,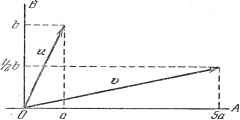

Рис. 4.1.

а если он находится на ОВ, то

ай = 0,5и.

Следовательно, OA и ОВ - два собственных направления а, а числа 5 и 0,5 - два соответствующих им собственных значения.

4Л.2. Сумма двух операторов. Если две операции а и р по отдельности приложены к вектору и, то сумма агг + Ви обозначается через

(а+Р)й.

Оператор а+р называется суммой операторов аир.

4.1.3. Произведение двух операторов. Пусть произведена операция а над результатом операции р, проделанной над и. Если можно перейти непосредственно от и к конечному результату действия обоих операторов при помош,и единственной операции -f, то оператор f называется произведением операторов а и Р:

)f?i = а фи).

Символически это записывается в виде

Т = ар.

Следует заметить, что в большинстве случаев оператор ар отличается от ра, поскольку порядок, в котором производятся операции, не безразличен. Это легко показать на следующем примере.

Пример 2. Дана прямая хх, точка О на ЭТОЙ прямой и некоторый вектор и (рис. 4.2). Операцию а определим как зеркальное отображение по отношению к прямой хх, а операцию р как поворот на 90 в направлении часовой стрелки.

Операция а над и дает вектор с а операция р над Vi - вектор w. Операция р над и дает вектор щ, а операция а над ©2 - вектор отличный от Wi (концы векторов w- и W2 симметричны по отношению к точке О).

Разность ар - ра назовем коммутатором операторов аир. Если коммутатор двух операторов равен нулю, то говорят, что операторы перестановочны. В этом случае

аР == ра.

4.1.4. Представление плоских преобразований с помощью матриц. Даны две оси прямоугольных координат, вектор и с составляющими и 2 и вектор V, полученный из и посредством преобразования а. Составляющие

и V2 нового вектора можно выразить как линейную функцию координат и, и 2 прежнего вектора. Получим два равенства, в которых коэффициенты а - числа:

Oj =а н, + а,2И2.

Рассматриваемое преобразование характеризуется таблицей коэффициен-. Она называется матрицей преобразования.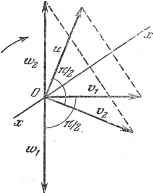

Рис. 4.2.

L--21

Пример 3. В примере 1 имеем

T/j = 5н, -j- О 2 272 = 0 Uj-f-0,5U2.

1 О

О -1

а операция р - матрицей

-1 О

4.1.5. Произведение двух матриц. Даны два преобразования а и В, характеризующиеся соответственно матрицами

Применив к вектору и преобразование р, а к полученному таким образом вектору V преобразование а, найдем вектор w. Определим матрицу

преобразования f, позволяющего непосредственно перейти от вектора и к вектору w. Имеем

l = Pll l + M2 i2 = Ml + M2-

Затем

Щ)2 = Kziil + °22i2

1 = ( иРп + <12P2l) 1 + ( 1112 + 1222) 2>

Рис. 4.3. ггг = (a2iPu+ 2221) 1 +( 2112+ 2222) 2-

Итак, матрица, определяющая преобразование а, иначе говоря, матрица произведения . имеет вид

пРп + 12Р21 t=llPl2 + Н--п

Мы узнаем здесь обычное правило образования элементов произведения двух определителей.

Пример 5. Рассмотрим обе матрицы из примера 4. Имеем

Ра =

1 .0 + 0-(-1) 0-0 + (-1).(-0- 1Ч-1 -о

Преобразование является зеркальным отображением вектора и относительно биссектрисы координатного угла zz, а преобразование - зеркальным отображением относительно биссектрисы W. Результаты преобразований, очевидно, симметричны по отношению к точке О (рис. 4.3).

Легко заметить правило образования элементов матрицы произведения аВ на приведенном примере произведения двух матриц, имеющих по две

Матрица оператора а здесь равна

5 О О 0.5

Пример 4. В примере 2 операция а представлена матрицей

О 1