Это - комплексная полная проводимость цепи, а 0(св) и 5(со) - соответ-

\г с

ственно активная и реактивная проводимости.

Пример. Требуется рассчитать комплексное полное сопротивление цепи (рис. 1.16) между зажимами А и В.

Здесь налицо два связанных между собой контура. Первый со-Рис. 1.16. держит конденсатор с емкостью Г,

комплексное полное сопротивление

которого Zj равно -Второй контур состоит из сопротивления/?, самоиндукции L и емкости С, подключенных последовательно. Комплексное полное сопротивление этого контура

Искомое комплексное полное сопротивление Z = . % , т. е.

1 ~Г 2

откуда

1 = /

2 + (Z.o, -1/С0))2

<p=arctg---arctg

--Lu,

1.2.8. Обобщение понятия комплексного полного сопротивления.

Рассмотрим электрическую цепь самого общего вида, состоящую из п отдельных контуров. Остановимся на контурах I м т.

в Z входит только через уш. Поэтому при переходе к комплексному сопряженному значению имеем

[Z (/ш)Г Z ([/О Z (-/со). Поэтому из формулы для Z(7u)) получим

Z(-уш) = /?(а,) -уХ(а,).

С другой стороны, если в выражении для Z(/tu) заменить со на -со,

Z (- Уш) = /? (- со) + jX (- со),

откуда

R (- w) = R (со) -четная функция со, Х{-ш) = - -(со) - нечетная функция со.

Величину, обратную Z(j(a), можно записать в таком виде:

1 -=K(/c0)=:G(c0)--/5(c0).

Пусть Lji, Rii, Сц - самоиндукция, сопротивление и емкость, включенные последовательно в контур Z; L, R и С - те же величины для контура т.

Обозначим через Li= L, Rim = Rmi im - mi самоиндукцию, сопротивление и емкость связи между двумя контурами lam. Для объяснения смысла этих величин рассмотрим цепь на рис. 1.17, состоящую из двух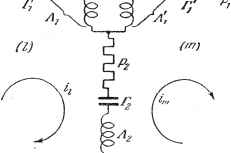

Рис. 1.17.

связанных контуров Z и т. В этом примере мы имеем при выбранном для токов положительном направлении

1 J 11 1,11 1 1

Im

fll-Р1 + Pi Р-тт-1 + 2- Pml-Plm- - Pi-

Вернемся к изучению цепи наиболее общего вида. Эта цепь описывается следующей системой дифференциальных уравнений:

-г Pnh

in-+Pinin + -fin

+ ... ... +

. di di

Rnni

где e e, .... e обозначают электродвижущие силы, приложенные к рассматриваемым контурам.

Приложим к контуру I электродвижущую силу е - Ее . Электродвижущие силы, приложенные ко всем другим контурам цепи, будем считать равными нулю.

Если положить

jLlmPlm--f-ZirnU)-

ТО система приобретает такой вид

Zn ( 1 + - + 2i (/со) g = О,

Обозначая через Djta) определитель системы, а через Mi(j(u) алгебраическое дополнение элемента ZiUw), получаем

Если положим

получим

D (М

imffm ИЛИ Eie = Zi

Величина

1т О ) называется эквивалентным полным сопротивлением цепи I по отноше-

то окончательно

нию к цепи т. Это - отношение комплексного напряжения, приложенного к цепи I, к комплексному току, текущему по цепи т.

Величина, обратная эквивалентному полному сопротивлению, иногда называется коэффициентом изоморфного отклика цепи т по отношению к цепи 1. Мы определили, таким образом, комплексное полное сопротивление, которое позволяет связать синусоидальный ток, текущий по одному контуру, с синусоидальным возбуждением, возникающим в другом контуре, связанном с первым. На практике можно вычислить эквивалентное полное сопротивление, выписав систему канонических интегро-дифференциальных уравнений рассматриваемой цепи и заменяя в этой системе знак дифференцирова-d

рования на

на усо, а знак интегри-1

После этого

/У Рис. 1.18.

остается решить систему полученных таким способом алгебраических уравнений.

Пример. Рассмотрим два связанных между собой контура, изображенных на рис. 1.18. Приложим к левому контуру электродвижущую силу Е = е . Дифференциальные уравнения системы принимают вид:

Соответствующая алгебраическая система будет

+ + J] h + >I/i 0.

Определитель ее

+ y) (- +-2 + ji) + -MK