-а\...а\

= KJ =

а\...а\ ... а\

Л.ЛЯ контравариантного вектора имеем

где суммирование происходит по нижнему индексу, означающему номер строки. Изменяя этот индекс, мы перемещаемся в матрице а вдоль /е-го

Тензор третьей валентности имеет компонент, которые могут располагаться в виде кубической таблицы. Существует четыре типа тензоров третьей валентности:

{П, {ti% (ш,

Произвольная -компонента наиболее общего тензора запишется в виде

с п ковариантными и т контравариантными индексами. Сумма иг+ге==р - валентность тензора, имеющего компонент. Это не означает, что математический объект , состоящий из г элементов, является р-валентным тензором в г-мерном пространстве. Определение тензора дается с помощью формул преобразования координат.

Пусть / 1*2 *т - произвольная компонента /7-валентного тензора, п раз ковариантного и т раз контравариантного в некоторой системе координат, а T/f-nt -соответствующая компонента того же тензора в любой дру-

гой системе координат.

Если /*2---.яг - компонента тензора, то преобразование компоненты t

в компоненту Т происходит по формуле

7.V y = 2 о;.... а; р ... pf2-v

Ui-n l...k -l n у m Г2---*/г

Наличие re ковариантных и т контравариантных индексов влечет за собой введение п множителей ант множителей р. Обратное преобразование имеет вид

ф-т 2 ... РК ...a T/ff.

\2n J...I i n h m \2-1п

Если преобразование в 7 и обратно не подчиняется этим формулам, то t не является тензором. Однако выяснение вопроса о том, является ли данная совокупность элементов тензором, путем установления применимости или неприменимости приведенных формул преобразования координат - длинная и сложная операция. Ниже (п. 5.1.15) мы рассмотрим более быстрый способ выяснения этого вопроса.

Б. 1.5. Матричная форма формул преобразования координат. Используя матричную форму, можно конкретизировать и упростить формулы преобразования координат для наиболее важных тензоров - тензоров первой и второй валентностей.

Пусть а - матрица преобразования координат: . .

столбца. Рассматриваемая формула имеет обычный вид произведения двух матриц (см. рис. 4.4), если ввести матрицу а, транспонированную по отношению к а; матричная формула преобразования контравариантного вектора имеет вид

Рассмотрим формулу преобразования для ковариантного вектора:

Так как индекс суммирования представляет, собой номер столбца для матрицы а и номер строки для одностолбцовой матрицы t, то матрица Т представляет собой произведение матрицы а на матрицу t. Формула преобразования ковариантного вектора в матричной форме принимает вид:

Рассмотрим случай дважды ковариантного тензора. Имеем В слагаемом

индекс суммы представляет собой номер столбца для матрицы а и номер строки для матрицы t, т. е. суммирование идет вдоль строки с номером I матрицы а и вдоль столбца с номером k матрицы t. Следовательно, речь идет об элементе произведения матриц А- at. В формуле

индекс суммы представляет собой номер столбца и для матрицы А, и для матрицы а. Следовательно, речь идет о произведении матрицы А на матрицу, транспонированную по отношению к а. Таким образом, матричная формула преобразования для дважды ковариантного тензора имеет вид

T=Aa-ata.

Для дважды контравариантного тензора имеем

Рассуждение, подобное предыдущему, позволяет получить для него следующую матричную формулу преобразования;

Г=р/Р при р = а-1. Наконец, для смещанного тензора имеем .

а в матричной форме

Т = at.

Замечание. Из приведенных формул не следует делать вывод, что квадратная матрица является тензором, так же как нельзя заключить, что совокупность двух чисел есть вектор на плоскости. Матрицы - это просто таблицы чисел или символов, никак не зависящие от преобразования системы координат. Тензором квадратная таблица чисел является только в том случае, если она состоит из компонент тензора

Можно сказать, что тензор второй валентности представляет собой в некоторой системе координат матрицу, элементы которой подчиняются

законам преобразования, свойственным компонентам тензора.

Аналогично тому, как элементы матриц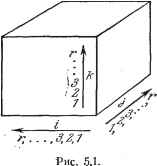

представляют собой координаты вектора в двух системах координат, причем свойства и существование этого вектора не зависят от системы координат, также и матрицы

содержат компоненты тензора второй валентности в двух системах координат. Свойства и существование этого тензора также не зависят от системы координат.

Аналогичное рассуждение применимо и к тензорам более высоких валентностей.

Тензор третьей валентности представляется в некоторой системе координат кубической матрицей (рис. 5.1). Она разлагается на г квадратных матриц, которые можно получить, разрезав куб на слои в соответствии с каким-нибудь из индексов.

Тензор четвертой валентности может быть представлен набором из г кубических матриц или из г квадратных матриц и т. д.

Для тензора любой валентности можно получить общие формулы преобразования в матричной форме, используя матрицы а, а и обратные им. В формулу преобразования для /7-валентного тензора входят р матриц пре-

) Мы видели, что при преобразовании координат матрица, связывающая два вектора, преобразовывалась по формуле (4) гл. IV. Эта матрица является тензором. Принимая во внимание сказанное в п. 5.1.3, заключаем, что указанная формула характеризует смешанный тензор.