В применении к двум индексам п ш k операция свертывания дает

- V ft

-ra - Уп

Второе свертывание, примененное к индексам j и т, дает

Мы пришли к контравариантному вектору. Если бы количество ковариантных и контравариантных индексов было одинаковым, мы получили бы в конечном результате инвариант.

Возьмем, например, два вектора противоположной вариантности © и к* и образуем тензор tf = uv. Производя свертывание, получим

ft к

величина с представляет собой инвариант - это скалярное произведение двух векторов и, v-.

Изложенные выше результаты дают критерий, позволяющий более быстрым способом, чем при использовании формул преобразования координат, установить, является ли совокупность элементов тензором (см. п. 5.1.4).

5.1.15. Установление типа тензора. Предположим, что нам встретилась величина, представленная совокупностью из элементов, зависящих, например, от трех индексов, которые меняются от 1 до г каждый. Мы не знаем, является ли эта совокупность элементов тензором и если да, то какова его вариантность, иначе говоря, положение его индексов. Обозначим рассматриваемую величину через t{l, k, т), где I, k, т - индексы, которые мы пока заключаем в скобки, так как еще не имеем возможности разместить их должным образом.

Попробуем произвести свертывание произведения этой величины на три вектора й, v, W (так как имеется только три индекса). Если мы найдем, что в результате свертывания произведения

2 t (i. k, т) uivw

получился инвариант по отношению к любому преобразованию координат, то величина t{i, k, т) представляет собой дважды ковариантный и один раз контравариантный тензор tf. . -

инвариантна. При полном свертывании любого тензора по всем индексам по-, лучается инвариант.

5.1.13. Умножение тензоров. Пусть и 5 - общие компоненты двух тензоров.

Произведением тензора г* (третьей валентности) на тензор 5 (второй валентности) является тензор p (пятой валентности), компоненты которого определяются формулами

тп т п

Произведение тензоров зависит от порядка сомножителей.

5.1.14. Свертывание произведения. Операция свертывания тензоров была описана выше. Посмотрим, что дает ее применение к произведению двух тензоров, например к приведенному выше тензору

Действительно, произведем произвольное преобразование координат. Так как при свертывании произведения получается инвариант, то

2(г, k, m)uivw = TU- I- n)UiViW\

ikm jln

Следовательно,

ikm jin

ЧТО указывает на тензорный характер величины t и дает его вариантность.

Пример. Перемещение точки представляет собой контравариантный вектор 8jc*. Какова вариантность силы?

Известно, что величина 8Л = 2 fk - это совершенная силой работа.

следовательно, скаляр. В правой части равенства стоит свернутое произведение силы на контравариантный вектор. Следовательно, сила представляет собой ковариантный вектор.

5.2. ТЕНЗОРЫ В КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ

5.2.1. Определение криволинейных координат. Криволинейные оси. Координатная поверхность. Пусть дано трехмерное пространство, отнесенное к прямолинейным осям Ох, Ох, Ох, причем е - соответствующие единичные векторы (рис. 5.2).

Отнесем то же пространство к криволинейной системе координат, т. е. свяжем старые координаты х, х, х с новыми Х, Х, Х соотношениями

X = fiX\ Х, Х). (3>

При этом новые координаты связаны со старыми обратными соотношениями

X = F (x\ л:2, хЗ). (4>

Дадим Х, Х, Х частные значения, соответствующие произвольной фиксированной точке О пространства, координаты которой выражены в старой системе координат формулами (3). Начиная с этой точки О, меняем значения и оставляем Х и Х фиксированными.

Точка, определяемая координатами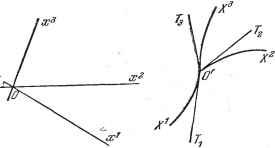

xi = fi(XK Х-, Х\ = /з(.А-1, Л2, Л-З),

Рис. 5.2.

описывает кривую, для которой уравнения (5) при условии, что изменяется только величина Х, являются параметрическими уравнениями. Эта кривая есть криволинейная ось ОХ, проходящая через точку О. Таким же образом можно определить криволинейные оси ОХ и ОХ.

Если в уравнениях (5) зафиксировать величину Х и изменять только Х и Л2, то точка опишет поверхность, которая определяется параметрическими

dxYdx-Yadx

Все эти формулы без всяких изменений применимы к случаю, когда старая система координат х\ e является также криволинейной системой координат.

Начиная с этого момента, мы будем вместо аффинного векторного пространства рассматривать метрическое пространство, так как теперь нам придется пользоваться понятием расстояния между двумя точками.

Пусть произошло перемещение dX по оси Х. Тогда соответствующие перемещения в старой системе координат будут

dx = -dX\ dx = -dX\ dx = dX\

Если предположить, что старая система координат прямолинейна и прямоугольна, то будет справедливо равенство

ds {dxf + (Jx2)2 + {dxf = (£j dXy,

аналогично

уравнениями (5). Это координатная поверхность ОХХ. Таким же образом .определяются координатные поверхности ОХХ и ОХХ.

Приведенные определения легко обобщить на г-мерное пространство. Криволинейные оси определяются с помощью г уравнений с одним переменным параметром, а координатные поверхности становятся гиперповерхностями, выраженными г уравнениами с двумя параметрами.

Знакомые нам формулы преобразования координат

xafX , X=Шx

применимы и в этом случае, но лишь к бесконечно малым перемещениям относительно точки О. В старой системе координат такие перемещения равны dxK в новой - dX .

Перемещения в новой системе координат можно считать происходящими по касательным ОТ к криволинейным осям Х .

Длины dX и dx выражаются с помощью локальных единиц длины, определяемых для каждой оси единичными векторами

Локальные единицы длины постоянны в бесконечно малом объеме вблизи точки О и меняются вместе с О. Действительно, имеем

Если к бесконечно малым перемещениям относительно точки О применить формулы преобразования координат, то эти формулы примут вид