5.2,2. фундаментальный метрический тензор. Пусть дано пространство, в котором мы можем определить расстояние между двумя бесконечно близкими точками. Если оси ортогональны, то, например, в трехмерном пространстве имеем

Если система координат косоугольная, то

ds- = idx) {dx) {e,f + {dx) (dx) {ef + {dx) (dx) {ef +

--(dxi)(dA:2)eje2Cos(ei, e-\-{dx){dx)eezosie, e-\--}-6363 cos (Cj. e3) + (:2)(dxi)e2ejCos(e2. e{)~\-

--(dx) (dx) 632 cos (3, e2)+(.*)(.*)3 ios(e3, ej).

В более общем виде

ds = 2 gik dx*.

gik = gkl = / /е cos (e,-, Cfe).

Так как величина ds инвариантна при любом преобразовании координат, то gi, - элементы дважды ковариантного тензора второй валентности. Тензор {giji) называется фундаментальным метрическим тензором.

Обозначим через g определитель, составленный из элементов g, g-\giii\- Пусть Gj - алгебраическое дополнение элемента g. Определитель g можно записать в виде

g=-gikOik=gikGik-

Первое выражение - это разложение определителя по элементам г-й строки, второе-его разложение по элементам -го столбца. Кроме того,

lAgikGik = если 1ф], к

так как при I Ф J получается определитель, имеющий две одинаковые строки, и:

S gikit = О если кф1.

так как при k Ф I получается определитель, имеющий два одинаковых столбца. Если положить

o-ik -ft - g

то g - дважды контравариантный тензор, потому что

gikg-U, I>gkig =bl

Определитель g тензора равен обратной величине определителя g тензора g,:

ggik\g-l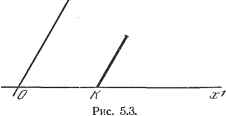

dz = dx dx ... dx,

a jlgl преобразуется в Vg- = l. Так как произведение

/id = jdP... dx

представляет собой в этой системе координат объем параллелепипеда с ребрами dx, dx, то величина Vjg ! rfx представляет собой тот же объем в произвольной системе координат.

5.2.5. Косоугольная система координат на плоскости. Пусть Ox и Ох2 - две неперпендикулярные оси (рис. 5.3), а е, а - соответствующие единицы длины.

Рассмотрим некоторую точку М на плоскости. Координаты этой точки можно получить, измеряя отрезки ОК и КМ ломаной ОКМ, параллельные

) Величина g - это определитель; - абсолютная величина определителя. Ве.аичина g - это общий элемент матрицы [gjj] тензора (gj) в рассматриваемой системе координат. Символом [ g. обозначается определитель этой матрицы.

5.2.3. Преобразование определителя g фундаментального метрического тензора при преобразовании координат. Имеем

где g - компоненты тензора в старой, а gi - в новой системах координат. Это выражение представляет собой не что иное, как общий элемент произведения трех определителей g-, Д и Д. Следовательно, определитель g равен

g=.gX.

или. иначе

Эта формула показывает, что Y\g\-скалярная плотность, а --скалярная емкость.

5.2.4. Выражение для элемента объема. Рассмотрим в г-мерном пространстве г раз контравариантный антисимметричный тензор, общая компонента которого равна

e-dxdxdx ....

где dx обозначает бесконечно малое перемещение по оси г, а ijk ... - некоторая перестановка из чисел 1, 2, .... г.

Известно, что все не равные нулю составляющие этого тензора имеют общее значение ± dx:

dz = Jx dx ... dx,

где dz-скалярная емкость. Поэтому произведение dz на величину Vjgl которая представляет собой скалярную плотность, будет независимо от выбора системы координат. Чтобы выяснить, что собой представляет это произведение, рассмотрим прямоугольную декартову *

систему координат. Тогда dz преобразуется в dz по формуле

осям координат Ox и Ох. Их истинные длины равны

ОК = еух\ КМ=--е2х\

где х и х - число соответствующих единиц длины в отрезках ОК и КМ. Следовательно,

ОМ =: (е, dxf + dxf + 2буб2хх cos 6,2,

где 6,2 - угол между осями Ох и Ох. Сравнивая с выражением

ds- = g {dxf + g22 {dxf + 2,2 dx rfx2.

получаем

gnCeJ. g22 = ( 2) g-12 = 6,62 cos 6,2-

Следовательно, тензор gj имеет вид

ёи gvA ( (l) 6,62 cos e,2\

.§21 g22/ V l 2COSe,2 (62)2 j

Элементарный объем tT/lg-l (в данном случае элемент площади) равен

da - dx dx6-62 Vl - cos 6,2 = 6-62 sin 6,2 dx dx.

5.2.6. Ортогональные криволинейные координаты в трехмерном пространстве ). Пусть дана точка М\ Мх, Мх , Мх - криволинейные оси, проходящие через эту точку, а е eg, б - локальные единицы длины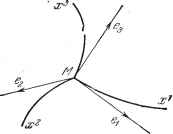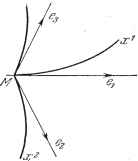

Рис. 5.4.

Рис. 5.5.

относительно точки М (рис. 5.4). Приращения координат dx, dx, dx соответствуют истинным перемещениям

ej dx, 62 dx, 63 dx,

откуда получаем тензор gi,:

[{6,f О О \

Определитель g равен Определитель g равен

{€2? О

о {6fJ

g = (£,6.63)2. . 1

{616263)

) Большое количество примеров ортогональных криволинейных координат приведено в п. 3.4.1 и последующих.