Здесь Еу, Е, £3-локальные единицы длины, отложенные соответственно по касательным ОТ ОТд, ОГд к криволинейным осям, проходящим через точку О (рис. 5.7).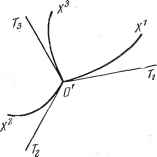

Рис. 5.7.

Элементы фундаментального метрического тензора, которые в старой системе координат равны

становятся в новой системе равными

Записывая подробно, получим

о Ъ giA\=gu {\f+g (cff+5-33 ( ?)

Следовательно, cos(ei, i)-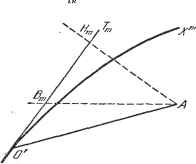

cos (£2. E2) -

со5(ез, з) =

Рассмотрим теперь вектор ОА с коор-Рис. 5.8. динатами а, а, в старой системе, в ко-

торой не различаются контравариантность

и ковариантность, а также с ковариантными координатами Л Л2, Л3 и с контравариантными координатами ЛЧ Л, Л в новой системе. Спроектируем ортогонально этот вектор на касательную ОТ к координатной линии ОХ , проходящей через точку О. Обозначим полученную проекцию через ОН (рис. 5.8).

Проведем через точку Л - конец вектора ОА-плоскость, параллельную плоскости, касательной к координатной поверхности, не содержащей линии ОХ. Пусть - точка пересечения этой плоскости с касательной 0Т .

V g Vg

2ofi

Vo-

В итоге получаем

2о5ЛГ

УОтт

Это хорошо согласуется с результатом, полученным для более частного случая прямолинейной косоугольной системы координат.

5.2.14. Частный случай ортогональных криволинейных координат. В этом случае 0Н=0В. Следовательно,

V Отш ИЛИ

т-тт

В векторном исчислении общее значение величин А Ymm - . рас-

V Gmm

сматривается как компонента а вектора ОА (индекс в этом случае не имеет ковариантного смысла).

Действительно, длина I вектора определяется выражением

Р=0 А А .

Поскольку мы рассматриваем криволинейные ортогональные координаты, то 0,а - О, если тф п, а G ,m = e\i. Поэтому

Если пользоваться прямолинейной прямоугольной системой координат, то

откуда и следует, что A YG , = АЕ = = = а .

v Gmm En

5.3. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ

5.3.1, Градиент. Рассмотрим скалярную функцию V. Компоненты градиента определяются формулой

dV ==-

Вектор градиент ковариантен. так как полный дифференциал dV - это

Имеем .

dV , dxK

5.3.2. Ротор (вихрь). Если а - ковариантный вектор, зависящий от координат произвольной точки, то компоненты ротора от векторной функции а определяются формулами

дар. dai

откуда bi, = - bfi- Следовательно, ротор а - это дважды ковариантный антисимметричный тензор (в трехмерном пространстве ротор можно уподобить осевому вектору).

5.3.3. Дивергенция. Рассмотрим формулу (см. п. 3.3.4) . .

dm - div (pV) dt,

где через dm обозначена масса, вытекающая в единицу времени из бесконечно малого объема di, р - плотность жидкости, а V--вектор скорости.

Необходимо уточнить природу величин, входящих в эту формулу, установленную для пространства, отнесенного к прямоугольной системе координат, чтобы затем можно было обобщить ее на пространство, отнесенное к произвольным криволинейным координатам. Вектор V контравариантен. Произведение элемента объема di (скалярная емкость) на плотность р представляет собой массу (чистый скаляр). Следовательно, р - скалярная плотность. Поэтому произведение pV будет векторной плотностью. Произведение дивергенции на элемент объема представляет собой массу. Следовательно, дивергенция будет скалярной плотностью.

Таким образом, операция дивергенции приложима не к вектору, а к векторной плотности а- Результат представляет собой скалярную плотность

3) = diva = Vi4.

I

5.3.4. Лапласиан (оператор Лапласа). Лапласиан - это скаляр, определяемый как дивергенция градиента скалярной функции V.

Градиент скалярной функции - это ковариантный вектор. Но, как мы сейчас видели, дивергенция приложима к векторной плотности, т. е. к произведению скалярной плотности на контравариантный вектор.

Фундаментальный метрический тензор позволяет получить градиент в контравариантной форме:

Соответствующая векторная плотность по оси t будет Следовательно,

инвариант, равный