Точка соединения нескольких ветвей называется узлом. Если два узла соединены накоротко, они образуют один узел (рис. 5.10). Замкнутая цепь называется контуром. Сложную цепь можно разложить на некоторое число простейших цепей. Между двумя простейшими цепями нет непосредственного электрического соединения, но существует электромагнитная или электромеханическая связь. Без этой связи обе простейшие цепи будут полностью независимы друг от друга. Контуры и ветви представляют собой расчетные

единицы цепи. Пусть 5, N, М, В - соответственно наименьшее число простейших цепей, узлов, контуров и ветвей, какое только можно различить в данной цепи. Между ними существует соотнощение

Ж = 5 -(10)

позволяющее определить минимальное число контуров М, которое необходимо рассмотреть для

ллллн

Рис. S.10.

расчета цепи. При непосредственном рассмотрении цепи это число не очевидно, но минимальное количество згалов N, ветвей В, простейших цепей 5 можно сразу увидеть из схемы цепи. Отсюда по формуле (10) определяем число М.

Каждая ветвь содержит некоторое количество пассивных элементов, совокупность которых образует собственное сопротивление ветви. Прохождение комплексного тока по этому сопротивлению вызывает появление комплексного напряжения на его зажимах. Обозначим через 2 отношение комплексного напряжения на зажимах к комплексному току в ветви - соб-ственное сопротивление ветви.

Если ветвь образована последовательным соединением индуктивности, активного сопротивления и емкости, то

Если исследуется не стационарный синусоидальный, а переходный режим, то величина Z становится функцией комплексной переменной р и получает следующий вид:

Если две ветви а к b соединены друг с другом, это означает, что прохождение комплексного тока в ветви а вызывает в ветви b появление комплексной электродвижущей силы, и наоборот. Сопротивление связи между а и b измеряется соотношением между этим током и напряжением. Обозначим его через Z. Сопротивление связи между b и а обозначим через Z,

Принцип обратимости требует, чтобы

аЬ Ъа

При электромагнитной связи

г г

Рис. 5.П.

в зависимости от рассматриваемой задачи.

Набор некоторого количества Z и электродвижущих сил в ветвях может оказаться недостаточным для полного расчета электрической цепи. Действительно, необходимо еще иметь возможность легко различать по схеме направление индуктивной связи между двумя ветвями. Существуют два способа последовательного соединения двух катушек индуктивности: потоки катушек могут быть либо противоположны друг другу, либо иметь одинаковое направление (встречное или согласное включение). Чтобы безошибочно показать это на схеме (см. рис. 5.11), самое простое - ввести нумерацию зажимов ветвей. Можно начать с любой ветви, зажимы которой нумеруются 1-2.

Рассмотрим какую-либо другую ветвь, индуктивно связанную с занумерованной. Если магнитный поток взаимной индукции, обусловленный током

влияющей ветви, пронизывая рассматриваемую ветвь, будет иметь направление, одинаковое с ее собственным потоком, обозначим ее зажимы 1-2 (согласное включение, рис. 5.11, а). В противном случае их следует обозначить 2-1 (встречное включение, рис. 5.11,6). При согласном включении смежные индексы различны, при встречном одинаковы. При отсутствии индуктивной связи нумерация не имеет значения.

Условимся, далее, относительно связи между направлением токов в ветвях и нумерацией зажимов. За положительное направление тока примем направление 1-2. То же правило будем (2) относить и к направлению элек-

£д д д д о тродвижущих сил.

V V v x I , Пример. Рассмотрим элек-

трическую цепь на рис. 5.12. Она содержит 3 узла, 5 ветвей и состоит из одной простейшей цепи. Следовательно, по формуле (10) минимальное число контуров равно 3. Предположим, что ветви й и / включены согласно, а а к b встречно. Предположим также, что электродвижущие силы, приложенные к ветвям d к /, имеют направления, указанные стрелками. Это обусловливает положительное направление токов в ветвях а, / и электродвижущей силы в ветви /. За положительные направления токов других ветвей могут быть приняты любые, однако их следует считать до конца вычисления неизменными. Если направление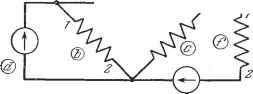

Рис. S.12.

) Однако принцип обратимости может не иметь места, если, например, одна из ветвей содержит электронный усилитель или вентиль и т. п. В этом случае ьФ-ьа,

тока в какой-либо ветви, принятое нами за положительное, не будет соответствовать действительному направлению тока, то это означает, что в результате решения мы получим для этой ветви отрицательную величину тока.

Если направления токов совпадают со стрелками на рисунке, то электродвижущая сила ветви d также будет положительна.

Ниже мы изложим метод быстрого составления уравнений, описывающих режим цепи. Подчеркнем, что речь идет о методе составления уравнений, а не об их решении.

5.4.2. Метод составления уравнений для цепи наиболее общего вида. Рассмотрим цепь наиболее общего вида. Примем токи, текущие в некоторых участках цепи, за вспомогательные неизвестные и с их помощью определим остальные токи цепи. Вспомогательные токи определяются следующим правилом: они должны протекать по таким участкам цепи, разорвав которые мы обесточим цепь. Это правило означает, что вспомогательные токи взаимно независимы в смысле первого закона Кирхгофа. Максимальное число таких токов равно минимальному числу контуров. Поэтому их называют контурными или независимыми токами в противоположность действительным токам, текущим в ветвях. Отсюда следует, что токи ветвей могут рассматриваться как результат наложения всех контурных токов, текущих по рассматриваемой ветви. Существенно определить для контурных токов положительное направление. Оно может быть совершенно произвольным, но, так же как определенное выше положительное направление для токов ветвей, не должно меняться до конца вычисления.

Обозначим контурные токи через 1, ..... а токи ветвей через

i*, ... (поскольку ветви были обозначены буквами а, ... и т. д.).

Можно рассматривать контурные токи как координаты вектора / в Л1-мерном пространстве. Назовем его контурным пространством или, проще, пространством o4i. Токи ветвей можно рассматривать как координаты некоторого другого вектора / в Д-мерном пространстве. Назовем его пространством ветвей или, проще, пространством Векторы I к I выражены соответственно матрицами

Примем, что они контравариантны, что оправдывает расположение индексов вверху. Токи ветвей можно выразить с помощью первого закона Кирхгофа или, что одно и то же, приравнять их сумме контурных токов, протекающих в ветвях. Получаем следующие выражения:

Каждый коэффициент С равен О, или -1 в зависимости от наличия тока в рассматриваемой ветви и от совпадения его направления с направлением, принятым для данной ветви за положительное.

Таблица коэффициентов С может рассматриваться как матрица преобразования, позволяющая перейти от вектора, представленного матрицей /, к вектору, представленному матрицей /. Назовем ее матрицей связи; при этом совокупность уравнений (11) запишется в матричных обозначениях) как

/ = С/.

) Матрица связи - это транспонированная матрица а п. 5.1.5.