Б пространстве tiM он будет равен

Z=.CZC =

Z-ba Z

~Zab+Z

Zab -66

- Zab + Z -

+ z

aa + Zj,

-fa bb

+ Zj - Zjt

ZjKi Z -f-+ Z/ -Z + -bZ + Z,/ +

Тензорное уравнение режима будет

Е = Z/.

Метод, изложенный в этом пункте, сводится к следующим простым приемам:

а) Тщательно вычертить схему изучаемой цепи, обозначить ветви, пронумеровав их зажимы в зависимости от связей, и обозначить имеющиеся электродвижущие силы.

б) Сосчитать узлы, ветви и простейщие цепи. Определить по ним наи-меньщее число контуров. Ввести столько независимых токов, сколько имеется контуров. Показать эти токи стрелками произвольных направлений.

в) С помощью независимых токов вычислить все токи в ветвях, пользуясь первым законом Кирхгофа и учитывая их направления. По полученной системе написать матрицу связи С.

г) Вычислить матрицы Е н Z с помощью формул

Е = СЕ, Z = CZC.

Отсюда выводится соотношение Е - Z/, решающее задачу.

Для дальнейших вычислений нужно знать структуру ветвей и, кроме того, более конкретно определить задачу. Если в задаче рассматривается только стационарный синусоидальный режим, то, например, электродвижущие силы и сопротивления будут иметь следующий вид:

-ya)L.

При этом, решая систему (19), найдем комплексные токи /.

Если требуется только составить систему дифференциальных уравнений, описывающих работу цепи, то следует заменить комплексные токи и напряжения мгновенными токами и напряжениями и подставить вместо знаков

дифференцирования и интегрирования j { )df соответственно ju> и

Если же требуется отыскать переходный режим, создаваемый несколькими электродвижущими силами hy{t), h2(t).....приложенными в момент

времени t~0, то следует ввести в систему (19) изображения электродвижущих сил fi{p)==hy{t), /2(р) = 2(0. *) и сопротивлений в виде

*) Употребляются еще следующие обозначения: f (р) h (t), f{j>)<h{t), f{p)<h it) (CM. гл. 8).

/? + - + Мы получим переходные токи как функцию времени, вычислив оригиналы выражений

например, путем применения теоремы разложения Хевисайда (см. п. 8.3.12).

Очевидно, что в случае постоянного тока речь идет лишь о решении системы линейных уравнений E=Z/, где элементы Z и Е-вещественные

ЛЛЛЛЛ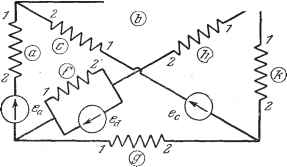

Рис. 5.15.

числа, выраженные соответственно в омах и в вольтах. При этом система (19; дает токи в амперах.

Последнее замечание: очевидно, что отыскание тензорным способом уравнений режима цепи, изображенной на рис. 5.13, невыгодно. Прямое

чЛЛЛЛЛ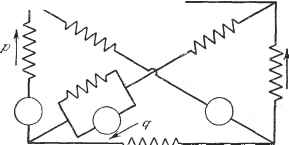

-5 -

Рис. 5.16.

вычисление было бы проще. Однако легко заметить, что по мере возрастания сложности цепи тензорный способ получает преимущество над прямым вычислением.

Другое важное достоинство вытекает из полного единообразия приемов описанного метода. Проиллюстрируем его на двух примерах цепей довольно простой структуры, для которых, однако, уже составление уравнений режима прямым методом было бы весьма затруднительно.

Пример 1. Приложим наш метод к цепи, изображенной на рис. 5.15.

а) Предположим, что ток, проходя по пути Ь, h, /, а, с, k. встречает индуктивно связанные ветви. Причем конструкция такова, что одни ветви будут иметь согласное включение (ас, а/, bf, cf, fk, bk), другие -встречное (ah, ch). Поэтому нужна нумерация ветвей, указанная на рис. 5.15.

б) Число ветвей равно 8, число узлов 5, число простейших цепей 1. Число контуров, следовательно, равно 4.

В качестве независимых токов выберем i, i, f, f. Они указаны на рис. 5.16 (буква i на данном и следующих рисунках опущена).

в) Остается вычислить токи ветвей как функции выбранных нами независимых токов. Результат такого вычисления показан на рис. 5.17.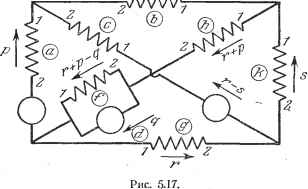

Заметим, что независимый ток i, проходящий по ветви а. имеет направление 2- 1. Так как положительное направление тока i будет 1 -2, то

[ - iP.

То же относится к ветвям Ь, f н k. Сделав это замечание, мы можем написать выражения для токов ветвей как функции независимых токов. Запишем их в виде соотношений между значками, опуская букву i *). Эти соотношения позволяют получить матрицу связи С:

*) Подобную запись будем применять и в дальнейшем.