т. е.

Если функция аналитическая, то это выражение тождественно равно нулю. Таким образом, полученная ранее функция переменных г и у не зависит от у, т. е. является функцией одного z. Обратное очевидно.

Отсюда следует, что дифференцируемая функция ср(/) вещественной переменной t, рассматриваемая как функция ср (л;-j-Уу), -аналитическая. Например, x-\-2jy - не аналитическая функция, х - y-2Jxy= - аналитическая.

1.3.4. Голоморфная функция. Аналитическая функция может быть как однозначной, так и многозначной. Однозначная аналитическая функция называется голоморфной *).

1.3.5. Криволинейный интеграл от функции комплексной переменной. Пусть f(z) - функция комп.аексной переменной z, С - непрерывная кривая, а Zq и Z - аффиксы концов этой кривой. Разделим кривую на произвольное

число частей с помощью промежуточных точек Zi, Zg, . -., z , z = z (рис. 1.20).

Пусть - точка, находящаяся ме-жду и z. Отрезок, началом которого является z , а концом г, обозначим через Дг.

Рассмотрим сумму

S == 2 / iPm) т-т=1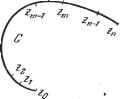

О Устремим п к бесконечности при условии.

Рис. 1.20. что наибольшее Дг стремится к нулю.

Если при этом сумма 5 имеет предел, не зависящий от выбора промежуточных точек, то этот предел называется криволинейным интегралом функции / (г) вдоль кривой С. Он обозначается так:

/ f{z)dz. с

Величина этого интеграла зависит не только от f (z), но и от формы кривой С.

*) Часто голоморфную функцию определяют как функцию, разлагающуюся в ряд Тэйлора. Отметим, что оба эти определения эквивалентны (см., например, [1], стр. 200-201).

Существует удобный критерий для проверки аналитичности функции. Функция комплексной переменной аналитична, если она, являясь по форме функцией двух независимых переменных хну, фактически зависит только от их комбинации х -\- Jy, т. е. является функцией одной независимой переменной Z. Легко убедиться, что это требование эквивалентно выполнимости условий Коши - Римана. В самом деле, если в выражении

Р(Х, y)+JQ(x, у)

заменим х на z - /у и по.аученную функцию переменных z и у частным образом продифференцируем по у, то находим

дуГ

Предположим, что длина кривой С конечна и равна s и что на этой кривой модуль f(z) не превосходит постоянной М. Тогда справедлива оценка

В самом деле.

г f(z)dz <Ж lim У Д2 .

ЧТО и доказывает оценку.

Если разложить f (z) и dz на их вещественную и мнимую части

то получим

/(г) = Р(х, y)-jQ(x, у), dzdx + Jdy,

f fiz)dz= J{Pdx - Qdy) + J J{Pdy-Qdx).

Как указано выше, интеграл, определенный таким образом, зависит не только от положения концов кривой С но и, вообще говоря, от формы этой кривой.

1.3.6. Теорема Коши. Пусть функция f{z) голоморфна внутри некоторой области. Тогда криволинейный интеграл от этой функции по любому замкнутому контуру, расположенному внутри области, равен нулю (рис. 1.21,

Итак, требуется доказать, что j f {z)dz = 0.

Применим формулу (5) к замкнутому контуру С, ограничивающему область S. Вещественные интегралы, стоящие в правой части этой формулы, преобразуем по формуле Грина *):

дР dQ

(6) (7)

Для голоморфной функции f(z) выполняются условия Коши - Римана, т. е. оба выражения (6) и (7) равны нулю. Таким образом, теорема Кощи доказана **). , .

) Это условие достаточно, но не необходимо. Действительно, существуют функции, не голоморфные во всех точках области и такие, что рассматриваемый криволинейный интеграл равен нулю. Примером может служить функция (z - при целых п > 1.

*) Эта формула является частным случаем теоремы Стокса (п. 3.3.9). **) Отметим, что при использовании формулы Грина существенно предположение о непрерывности частных производных функций Р и Q. Это предположение для справедливости теоремы Коши является излишним (см. [1], стр. 148-155).

Замечание. Доказанная теорема справедлива не только для простых контуров типа, изображенного на рис. 1.21, а. Она верна также в случае.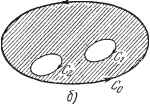

Рис. 1.21.

когда внутри области, ограниченной контуром Cq, имеются дырки, окруженные контурами С и т. д. (см. рис. 1.21,6). В этом саучае под контуром С в теореме Коши надо понимать сложный контур, состоящий из наружной кривой Cq. проходимой в положительном направлении (против часовой стрелки), и всех внутренних кривых Cg и т. д., проходимых в отрицательном направлении (по часовой стрелке).

В случае голоморфности /(г) интеграл (5) зависит только от положения начала и конца кривой С и не зависит от формы пути интегрирования. Для доказательства достаточно применить теорему Коши к замкнутому контуру С-\-С, где С - любая кривая, соединяющая концы кривой С.

Замечание. Вещественный криволинейный интеграл не зависит от формы пути, если он берется от функции, представляющей полный дифференциал. Условия Коши-Римана совпадают с условиями полного дифференциала для (5).

1.3.7. Формула Коши. Пусть f (z)-функция, голоморфная в замкнутой области, ограниченной контуром С, а Zq - внутренняя точка области

(рис. 1.22). Докажем, что имеет место формула Коши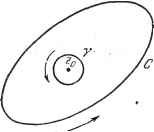

где контур С обходится в положительном направлении. Действительно, функция голо-

морфна во всех точках внутри контура, кроме точки Z = z. Исключим из рассматриваемой об-р,(, 22 ласти небольшой круг с центром Zq и радиусом р..

Окружность его обозначим через f (см. рис. 1.22)..

Функция голоморфна внутри кольцевой области, ограниченной Сиу. Z -

Если перемещаться по С и по 7 в положительном направлении, то по теореме Коши

Р1нтеграл слева не зависит от р. Следовательно, интеграл в правой части также не зависит от р. Имеем

J Z - Zo

J Z - Zo ./ Z - Zo .1 - Z - Zo