результатом § 26, имеем

~z{t) A z {t),

s(0= [А - KB]2{t)-~p-

z it).

Отсюда сразу следует, что собственные чис;[а замкнутой системы есть собствешшо числа системы со стационарной обратной связью по состоянию (матрица [А - В К]) плюс собственные числа идентификатора (матрица А). Это следует из представления матрнцы системы (2) в виде

МО МО J

> \А - ВК]

Эта теорема завершает исследование задачи конструирования устойчивого регулятора нулевого состояния. Рассмотрим подробно ряд примеров конструирования асимптотически устойчивых регуляторов.

Пример. Два интегратора, охваченные положительной обратной связью, имеют следующие уравнения;

1 - ai У

[1 0].

Согласпо теореме 1 для этой системы можно выбрать цепь обратной связи, содержащую два динамических элемента, и такую, что замкнутая система 4-го порядка будет иметь произвольно заданный характеристический многочлен. Это можно сделать потому, что система является управляемой и идентифицируемой. Коэффициенты цепи обратной связи вычисляются по формулам (1). Структура этого регулятора приведена на рис. 27,2.

Согласно теореме 2 для этой системы можно выбрать обратную связь первого порядка такую, что замкнутая система будет иметь произвольно желаемый характеристический многочлен 3-го порядка. Построим такой регулятор.

1. Вычислим характеристический многочлен матрицы А ФА (Я) = Я - 1; tti - О, 2 = - 1-

2. Зададимся многочленами; фу (Х) ~ Х X -\-

и ф {X) = X + Р, которые характеризуют динамику

системы, охваченной стационарной обратнойсвязью по состоянию, и динамику идентификатора состояния соответственно.

3. Так как пара матриц {А, Ь} имеет каноническое представление, то компоненты вектора к сразу вычислим по формулам 1 = 72 - 2, 2 7i - i > следовательно,

4. Теперь необходимо перейти к базису, в котором пара {Ау с} имеет идентификационное каноническое иредстав-лепие. Переход к идентификационному каноническому представлению осуществляется с помощью матрицы

1 о1

Р1 =

преобразование с помощью этой матрицы всех матриц системы дает:

А: - РАР- =.

Ь : РЬ -

с:= сР-1 - [О 1], к:= кР-1 - [Yi- 72+1]-

5. Остается преобразовать матрицы системы {А, Ь, с, к} с помощью преобразования

1 -.

1 3 О 1

,0 1.

Б результате получим матрицы регулятора вида А: =

А р О 1

- 3 ~ -Ь 1

1 3

b : = РЪ =

к: =кР-1 = [Г1, 72 + 1] с : = ср-1 - [О 1]

1 Р

О 1

1 р ! О 1

-[Г1>?Т1 + (Т2 + 1)], - [О 1].

На рис. 27.3 приведена структурная схема обратной связи вместе со структурной схемой объекта. На рис. 27.4 тот же регулятор изображен в соответствии с общей схемой рис. 27.1.

Стабилизация неустойчивого объекта 4-го порядка.

Рассмотрим задачу выбора параметров регулятора для

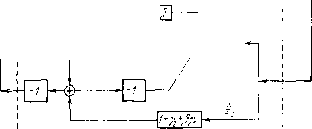Pnc. 27 3.

0 M\

cocmoQHjp Д иобратиая сЗяь

.7,-

Рис. 27.4.

Рис. 27.5.