Чтобы сделать это, заметим, что задачу вычисления оптимального управления можно трактовать как задачу решения линейного интегрального уравнения и

X (п) = Ф (0, 6) В (а) п (3) - [Ф (0, i) xi - Хо].

Здесь L (и) определяет линейное преобразование евклидова бесконечномерного пространства т-ок непрерывных функций, которое мы обозначили [t, t], в линейное п-мерпое евклидово пространство Е, или

L{n): С 10, i[->E . Напомним, что скалярное произведение в Е : <;xi, Xg) = = Х1Х2, а скалярное произведение в Uq, ti):

<ui, U2> = 5 ii)2 d-г

Заметим далее, что оператор L*, сопряженный к L, имеет вид

L* (X) = B{t)0(f ti)x, где X е Е\ и поэтому преобразование LL* просто равно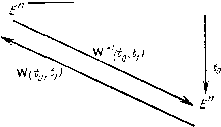

Рис. 34.2.

W {ffi, tl). Если эта матрица обратима, то в соответствии с теоремой 2 § 32 выбор

Uo (t) = -~B{t)0{to,t)W- (to, tl)

минимизирует <u, u> для L (u) = x. Приведенная на рис. 34.2 диаграмма иллюстрирует идею этого доказательства.

где С - емкость, i (t) - ток в цени, R - сопротивление. Энергия, рассеянная на сопротивлении в интервале [О, fi],

равна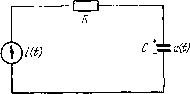

-1

Ri (t) dt.

Пусть требуется найти i {t) такое, чтобы и (0) = = Uq, и (fl) = Mj, а энер-Рпс 34.3. гия, рассеянная иа сопро-

тивлении, была бы минимальной. Мы хотим минимизировать

J = (t) dt.

Грамиан управляемости в этой задаче имеет вид W (О, fj) = = и оптимальное движение в соответствии с результатом теоремы 1

Н (t) = - (mi - щ) = const.

Минимум рассеянной на сопротивлении энергии реализуется при постоянном токе. Если и = О, то простой расчет показывает, что отношение энергии, накопленной в цени, к энергии, затраченной за время tj в оптимальном режиме, равно 1/(1 -- 2RClti). Это отношение минимизирует эффективность этой цени как накопителя энергии.

Общвй случай терминальной задачи. Последний шаг в решении задачи управления с квадратичным критерием качества состоит в решении терминальной задачи, когда L в критерии оптимальности отлична от нуля. Процедура решения состоит в комбинировании полученных ранее результатов.

Рассмотрим простои пример использования доказанной теоремы. Пусть даиа электрическая цепь (см. рис. 34.3). Уравнение движения этой системы

Си (t) = i (t),

Пусть уравнение движения системы

x{f) =Л (t)x (t) + В (f)nif),

а критерий качества и

J = 1{а (О н (t) + х (f) L (t) X (f)} dt. (3)

Решение задачи выбора оптимального и (t) снова зависит от решения уравнения Риккати

к (t) = - A{t)K it) - к {t)A (t) -I- К {t)B {t)B{t)K{t) -

~L{t). (УР)

Однако граничные условия в этом уравнении, как будет показано ниже, не являются теперь жестко фиксированными.

Теорема 2. Предположим, что существует симметрическая матрица Ki такая, что решение К {t, К, матричного уравнения Риккати существует на интервале 0 1- Тогда дифференцируемая траектория х {t), определенная на интервале t t, минимизирует критерий качества (3) для дифференциального уравнения X {;) = А {t)x it) + В (i)u [t) и граничных условий х [t = = Xq, X (i) -- х тогда и только тогда, когда она минимизирует величину

Ji = \\ it)\{t) dt,

для дифференциального уравнения

X (t) = [А (t) - В {t)B{t)K (t, Kl, ti)]x(f) + B(f)y(t)

и граничных условий x (to) = x, x = x. Более того, вдоль любой траектории, удовлетворяющей граничным условиям, выполняется равенство

J = Ji-\xK (to, Kl, ti)xa ~ x{ti)KiX (tl).

Доказательство. Если подставить уравнение (t) = А {t)x (f) + В (t)u (t) в равенство леммы 1 § 33,