МЫ ВИДИМ, ЧТО К {t, о, tj) существует на любом интервале 0 < < к-

Чисяевиое интегрирование уравнения Риккати на конечном временном интервале. Из леммы следует, что решение уравнения Риккати для стационарной системы {А, В, С] с критерием оптимальности

(у it)y{t)-\-u{t)u{t)}dt

представимо в виде К (t) = {Фз1(0, t) ~

Ф (0, 0(0)}{Фи(0, t) +

+ Ф1А0, t)my\

(0) - - (О, h) ФпФ, h), О < f <

Фи{0, () Ф1з{0, .Ф31(0, О Ф22{0, oJ

А ~~ВВ-

(2) (3)

Поэтому матрицу К (t) можно вычислить, если вычислить значение е. Используе.м для вычисления этой матричной экспоненты алгоритм § 13. Такой подход предложен в работе [61]. Тогда

ехр {Dh) = Л -h О {h), где

и О ih) означает ошибку аппроксимации ряда для экспоненты, имеющую порядок h.

Если матрица Л вычислена, то требуется матричных умножений для вычисления ехр {Dt) в точках h, 2h, Ah, Sh, . . ., 2%. Причем, очевидно, ехр {2hD) = Л-Л = = Л, ехр {2hD) = ЛА = \ , . ехр (2) = - д2К-1дйЬ 1 дзЕ рд, целое число, выбираемое

так, чтобы шаг интегрирования h = tii2 был достаточно малым, чтобы обеспечить малую ошибку аппроксимации О {h%

После вычисления матрицы ехр (Z>i) при О i значение К (0) вычисляется по формуле (3), а значение К {t) - по формуле (2).

Этот алгоритм обеспечивает высокую скорость сходимости вычислений. Однако он плохо работает при fj-j-oo,

поскольку в этом случае столбцы матрицы Фа2(0, t) становятся линейно зависимыми и матрица К (0) не определена.

Общее время вычислений, требуемое для расчета К (t), приблизительно равно (25 ~Ь 12 Щртъ, где fx - время операции умножения, к обычно варьируется в пределах 5-

20. Приблизительнообщего времени занимают вычисления обратных матриц [61].

Итерационное решение алгебраического уравнения Риккати. Рассмотрим алгоритм решения уравнения

AV \- VA - VBBV Ч- СС - О, (АР)

основанный на итерационной процедуре, построенной при доказательстве теоремы 1 § 35. Оп состоит из следующих шагов-

1. = BVm-ir

2. Ат-АВК;,.

3. Вычисляем Vm как решение линейного матричного уравнения

a;f -Ь VA -Ь СС 4- КшКгг. = 0.

4. Проверяем условия окончания вычислений

Вычисления 1-4 осуществляем при m = 1, 2, . . Чтобы начать вычисления, необходимо подобрать таким образом, чтобы матрица [А - BKq] была устойчивой

Сделаем в связи с этим алгоритмом ряд замечаний.

1. Построенная процедура подобна методу Ньютона решения нелинейного уравнения / (х) = 0. Она имеет простую геометрическую интерпретацию в скалярном слае. Тогда уравнение (АР) является простым квадратным уравнением. Решение этого уравнения методом Ньютона строится по формуле

Из которой следует

(2А - 2BV) Vmn + BVl 4- О,

Это уравнение совпадает с линейным уравнением

JrVBBVO,

решаемом на каждом шаге итерационного процесса. Геометрическая интерпретация итерационного решения уравнения (АР) в скалярном случае дана на рис. 36.1.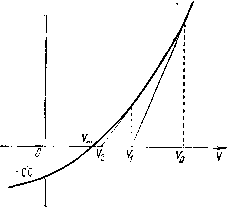

Рис. 36.1.

2. Известно, что метод Ньютона обеспечивает квадратичную сходимость вблизи точки решения. Это свойство сохраняется и в матричном случае. Можно показать [661, что в условиях приведенного алгоритма

где а - положительное число.

3. Для выбора начального значения можно использовать алгоритм построения устойчивого регулятора по состоянию, приведенный в § 23. Решение линейного матричного уравнения Ляпунова можно реализовать с помощью процедуры, приведенной в § 16.

Задачи. 1. Найти управление, которое приводит систему

u(t)