Это уравнение называют правилом композиции для переходной матрицы. Воспользуемся для доказательства этого правила определением переходной матрицы Ф (t, t) = = X {t)X~ (g. Непосредственная проверка дает

Ф {t, to) = X {t)X- {to) = X {t)X- {t,)X {t,)X~ it,) =

- Ф {t, g Ф {t to).

Диаграммы, которые иллюстрируют альтернативные линейные преобразования, называются коммутативными диаграммами. Для правила композиция такая диаграмма приведена на рнс. 10.1. Она свидетельствует о том,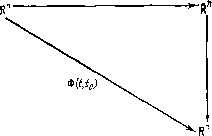

Рис. юл.

что из состояния Хо можно перейти в состояние Xj либо с помощью линейного преобразования Ф {t, t), либо последовательно применяя два линейных преобразования: сначала Ф {t, to), переводящее Хд в некоторое промежуточное состояние Xj , п далее преобразование Ф {i, t), переводящее х в требуемое состояние х. Мы и в дальнейшем будем пользоваться коммутативными диаграммами для иллюстрации формул подобного типа.

Преобразование координат. Если уравнение х {t) ~ = А {t) X {t) имеет переходную матрицу Ф {t, to) и сделана невырожденная замена переменной z {t) = Р {t) х (t) \ Р (t) \ ф О при всех t, то как преобразуется переходная матрица?

Предположим, что Р {t) и Р~ {t) существуют, и про ведем указанное преобразование переменных:

z{t) Р (t) X {t) -h Р (Ox {t) - [P {t) A (t) + P{t)]x{t) = = [P {t) A {t)P- {t) + P (0 P- (t)] z {t).

Кроме ТОГО,

X (О = Фа (t, Хо = (t) ъ {t) = (О Ф[РАр-+рр-]2о =

Нами доказана

Теорема 2. Если Р {1) дифференцируема и существует р- {t), тл)

Фа ( о) = Р- {i) Ф1РЛР-+РР-] о) Р (о)- О

Как и в предыдущем случае, этот результат удобно представить в виде коммутативной диаграммы, приведенной на рис. 10.2.

Рис. 10.2.

Неоднородное уравнение. Рассмотрим теперь решение неоднородного уравнения

±{t) А {t)x{t) + i{t). (ЛН)

Снова полезно провести аналогию с линейными алгебраическими уравнениями. Вспомним, что общее решение уравнения Ах = Ъ состоит из двух частей: частного решения этого уравнения и элемента х, принадлежащего ядру матрицы А, т. е. удовлетворяющего однородному уравнению j4x = 0. Другими словами, оно является суммой частного решения Xj и решения однородного уравнения Xg. Перепишем уравнение (ЛН) в виде

[DE ~ А (01 x (О = f (О, О Jf

(0-z(g-Ф(,a)f(a)d5

и далее

X (О = Ф (t, t,) Гх (о) + 5 Ф (0,0) f (в) d:

= Ф{t,t,)x,{ф{t, o)f{o) do.

Полученное равенство называют формулой Коши или формулой вариации постоянных. Проделанные вычисления позволяют сформулировать следующее утверждение.

Теорема 3 (формула Коши). Если Ф {t, ц) - переходная матрица для х (i) = А (t) х (t), то единственное решение уравнения (ЛН) при начальном условии х (t) - = Xq дается формулой

X (О - Ф {t, t,) Хо -I- J Ф {t, 0) f (5) do. (ФК)

Отличие от алгебраических уравнений состоит в необходимости вводить начальные условия. Эти начальные условия жестко фиксируют решение однородного уравнения, которое нам уже известно, х (() = Ф (t, (,)хп. Остается найти частное решение неоднородного уравнения. Если А - О, то имеем

и, интегрируя, получим

x(0-x(?o)-bSf(o) do.

Преобразуем теперь уравнение (ЛН), введя замену переменной Z (t) ~ Ф (tg, t)x (t), где Ф {t, t) - переходная матрица для А. Это преобразование исключает зависимые переменные справа и дает

(0 = ф-М дс(0-ф(о, ОМО-

Отсюда сразу получим