В понятие пространства состояний в теории управления. Напомним, что выбор обобщенных координат динамической системы отнюдь не является однозначным.

Рассмотрим электрическую день рис. 14.1, Известно, 410 если задан начальный ток в индуктивности и начальное напряжение на емкости, то для любого закона

Рис. 14.1.

U {t) изменения входного напряжения выходное напряжение у {t) можно определить единственным способом. Поэтому ток в индуктивности и напряжение на емкости можно рассматривать в качестве переменных состояния. В цени рис. 14.2, если известны все напряжения на емкостях, которые мы обозначим через х-, х х, то поведение цени единственным образом определено для любого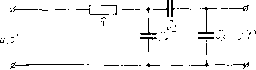

Рис. 14.2.

входного воздействия. Поэтому напряжения на емкостях дМожно рассматривать как переменные состояния. Рассмотрим, однако, эт} цель подробнее, Ло закону Кирхгофа пмеем х- (t) -f х-, (t) -\- х (t) = О для всех t. Псэтому, если любые два напряжения из {х-, х, х} известны, то третье определяется однозначно. Другими словами, два напряжения на емкостях тоже являются состоянием. Если же Б качестве состояния выбраны все три напряжения, то имеется избыточность в определении состояния. Естественно так стремиться выбирать состояние системы, чтобы оно содержало бы наименьшее число переменных.

Как указывалось выше, выбор неремоппых состояния не является единственным. Фактически путем замены базиса в пространстве состояний можно ввести новые неременные состояния, поэтому существует бесчисленное число способов выбрать эти переменные. Обычно употребляются лишь некоторые из этих способов, либо те, которые дают математические преимущества в исследовании модели системы, либо тс, которые имеют ясный физический смысл.

Уравнения состояния и передаточная функция. Основным ноиятпем теории регулирования является понятие передаточной функции. В дальнейшем будем решать задачи управления линейными объектами, пспользуя их описание в пространстве состояний. В рамках этого подхода решение ряда традиционных вопросов теории управления выглядит существенно проще. Кроме того, матричное описание систем удобно с точки зрения использования вычислительных методов алгебры и программирования задач на ЦВМ.

На рис. 14.3, а дано графическое изображение системы с одним входом и одним выходом, описанной с помощью

U\t -I

Рис. 14.3.

передаточной функции W {р), а на рис. 14.3, б - с помощью уравнений состояния (ЛС).

Йри сравнении описания системы в пространстве состояний и описания с помощью передаточной функции возникает вопрос: когда эти описания эквивалентны? Связанный с этим вопрос: как перейти от одного описания к

Другому? По этому поводу заметим следующее. Поскольку передаточная функция отрая-;ает только соотношение между входом и выходом системы, всегда имеется определенный произвол в выборе переменных состояния системы, заданной с помощью передаточной функции. С другой стороны, если известно описание системы в пространстве состояний, то передаточная функция сразу определяется, и притом однозначным образом. Тот факт, что описанию системы в пространстве состояний отвечает единственная передаточная функция, а передаточной функции системы соответствует бесконечно много представлений в пространстве состояний, свидетельствует о том, что описание спстемы в пространстве состояний является более общим. Вычислим передаточную функцию стационарной системы с одним входом и одним выходом. Предположив, что начальные условия равны нулю, возьмем преобразование Лапласа обоих уравнений (ЛС):

рх(р) = Ax{p) + bii{p), У{Р) = сх(р).

Из первого уравнения, предполагая существование обратной матрицы, имеем

X (р) = [рК - bu(p).

Отсюда сразу получим

у{р) =с [рЕ -Л]~ Ьп (р).

Коэффициент перед и (р) равен передаточной функции системы. Следовательно,

W (р) = с [рЕ - Л]- Ь.

Рассмотренный прямой метод не всегда пригоден для практического использования, поскольку требует вычисления обращения матрицы. Проще получить передаточную функцию, преобразуя структурную схему системы (ЛС). Пример такого преобразования для системы, заданной матрицами

Г О 11 01

представлен на рис. 14.4.