Мы воспользовались свойством переходной матрицы Ф {t, о) = Ф {t, to) Ф {to, а).

Используя теперь свойство 4 оператора W {t, t{) (см. теорему 2 § 19), согласно которому

W {to, t,) = W {to, О + Ф {to, tW {t, tl)Ф {to, t), получим

x{t)=Ф {t, to) Ф {to, t)W {t, tl)Ф {t t)x =

= W {t, ti) Ф {to, t)x.

Подставляя это выражение в формулу для управления, указанную в условии теоремы, замечаем, что

XLt) = -BW~ {t, tW{t, tl)Ф {to, t)z = -ВФ {to,t)x

в точности совпадает с управлением Пх (О-О

Из доказанпой теоремы следует, что матрица обратной связп К {t) -BW~ {t, tj) обеспечивает двюкение системы из (0) ) в (1, 0).

Замечание. Закон управления п (t) ~ = -BW~ {t, ti)x {t) редко используется на практике, так как К {t) оо при t t-. Это связано с условием точного попадаппя в начало координат за конечное время переходного процесса. Кроме того, полученный закон управления не является стационарным. Основной вывод доказанной теоремы состоит в том, что для полностью управляемого стационарного объекта можно не только выбрать управление как функцию времени, обеспечивающее переход системы в начало координат за любое конечное время, но и реализовать это управление в виде (к сожалению, нестационарной) обратной связи.

Нестационарные объекты. В случае нестационарной системы матрица W {t, t) (грамиан управляемости) может пе иметь обратной при пекоторых t даже в том случае, если система управляема. Однако и в этом случае управление в виде обратной связи, которое удовлетворяет условиям теоремы, сзществуот и имеет прежний вид

u{t) = -В {t)W{t, ti)x (О,

где - псеедообратная матрица оператора W {t, t-, которая определена при всех t как решение матричного

Рпс. 21-1.

является полностью управляемой- Выберем в качестве конечного момента време1[н t, тогда оператор W (/, /,} имеет вид

W{t,ti) =- \L{f)df при 1,-.1 и.

Для всех значений времени * / оператор

W {t, = О и, следовательно, но имеет обратного, хотя система и является полностью управ.ляемой. J Гоэтому формулой

и(0 ~В {t)W- {t, t,)x(t)

воспользоваться нельзя. Чтобы обойти эти трудности, используется понятие псевдообратной матрицы.

Пример 2. Полученное уравнение несгационар-ного линейного регулятора трудно использовать па практике, так как W (t, tj) оо прп t ~> f. Правда, при этом X (t) о, и управляющее воздействие п (О = = -В {t)W~ (f, tx)x {t) остается конечной величиной, во

уравнения WXW = W, такое, что отобран;ение X [t, t) при каждом 1 является кусочно-ненрерывным. Подробности о построении и свойствах псевдообратной матрицы имеются, например, в типе MU). Здесь я;е мы только пропллюстрирлсм на простом примере трудности, которые могут возникнуть при обращении матрицьс V {t, t-x) в нестационарной системе.

Пример 1. Пусть дана скалярная нестационарная система х (t) = b {t)u [t). Переходная матрица этой системы равна 1 (Ф {t, to) = 1). Пусть функция b (t) пмеет вид, представленный па рнс. 21.1. Система в момент

реали-зовагь его затруднительно, так как придется умножать бесконечно боль7шге величины на бесконечно малые, В припиипе, однако, зта обратная связь может быть иснользована для пост]юепия многоканального или им-пульспою регулятора следующим образом.

Пусть состояние системы изменяется под действием помехи, спектр частот которой ограничен частотой (Од. Выберем период Т подключения регулятора к объекту так,

чтобы он был одного порядка с величиной -х-, а время

нодключсыпя регу.чятора выберем так, чтобы <<;;; Т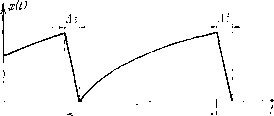

Рис. 21.2.

При этом условпи можно не учитывать действие помехи в период регулирования. Схематически процесс регулирования представлен на рис. 21.2,

Рассмотрим конструирование подобного регулятора для объекта второго порядка х {t) ~ и (t). Как было показано ранее, матрицы такого объекта имеют вид

Переходная матрпна

Ф (О, t) -

с - [1 0].

Нетрудно показать, чю W {t, имеет вид

(1 -- if (/г - Оп