а значит,

г 13

(h - t)- (fl -0 - В 4

Jh - ty- {ti - i) Следовательно, матрица обратной связи

-6 4

Структурная схема этого объекта, охваченного обратной связью, представлена па рис. 21,3.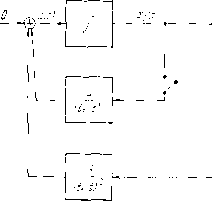

Рис. 21,3.

На практике основной интерес представляют стационарные обратные связи: К = const. При решении задачи регулирования с помотдью такого класса обратных связей нам придется отказаться от требования точного попадания системы в начало координат за конечное время регулирования. Единственной разумной заменой этого требования может быть требование асимптотической устойчивости системы относительно начала координат. Ниже будет показано, что управляемая стационарная линейная система может быть сделана асимптотически устойчивой с помошью стационарной обратной связи, причем характеристический многочлен замкнутой системы можно выбирать по своему усмотрению.

Прдс чем приступить к решению этой задачи, мы обсудим вопрос о выборе базиса в пространстве состояний линейной стационарной системы.

Задача. Для системы

*1 [П L*2 (О J

XI (t) х2, {t)

вычислите управление в виде обратной связи, которое обеспечивает перевод любого события (О, х) в событие (f, 0).

§ 22. Канонические представления

Полученные до сих пор результаты не были связаны с каким-либо конкретным базисом пространства состояний. Бее они были справедливы для любого базиса, в котором записаны матрицы А, В, С, Ф, W. В дальнейшем нам удобно будет выбирать вполне определенный базис в пространстве S с тем, чтобы матрицы системы имели хорошую (каноническую) форму.

Это будет полезно в двух отношениях. Во-первых, канонические представления матриц системы имеют минимальное число ненулевых элементов и потому удобны при вычислениях и при моделировании системы. Во-вторых, канонические представления существенно упрощают, как мы увидпм в дальнейшем, доказательства основных теорем о свойствах обратной связи в лпнейной стацпонарной системе. С их помощью будут получены простые алгоритмы вычисления структуры п коэффициентов регуляторов, обеспечивающих желаемые динамические свойства замкнутой системы.

Замена базиса в пространстве состояний. Для линейной системы

k{t)= Ax{t)-{Bu{t), y{t)Cxit)

рассмотрим невырожденное линейное преобразование переменных X = Рх, где Р - несингулярная матрица размером п X п. В новых переменных уравнения спстемы примут вид

X = РАР-Х + РВи,

у = СР-Ч

X Лх 4- п, I у = Сх.

Преобразованные матрицы системы вычиоляются о формулам

А РЛР-, В РВ, с - СР~. I

Матрицы Л и А подобны, и зпачш, нх характеристические многочлены совпадают.

Напомним, что столбцы матрицы Р~ содер/кат координаты новых базисных векторов относительтто старого базиса. Если новые координатные векторы известны, то матрицу А в новом базисе {cj} можно вычислить по правилу (см. § 7): (-Й столбец матрицы Л в базисе {е,} состоит из координат вектора А в этом базисе.

Соотношение между входом системы и (t) и выходной величиной у [t) Б исходнот ! и преобразовапнот ! сис-гемах останется неизменным. Одним и тем же входным воздействиям будут соответствовать одинаковые выходные величины. Это можно показать непосредствеипо, выписав выран;ение для выхода у [t) в обеих системах. Для исходной спстемы имеем по формуле Кошт!

y{t) = C%{t) - с\е.-о>Ха + \ еМо-)Ви{з)(Ь

Для преобразованной систомы, атталогично, имеем но

Подставляя эти равенства в формулу для j (/). убедимся, что

У (О - ИО.

Линейные невырожденные преобразовании коордиттаг в пространстве состояний лпттейтюй системы но сутцеста соответствуют обычным методам преобраовант1Я структурных схем в теории регулирования. Пменпо, каждому разрешенному (не пзменяюш,еу1у перодаточпот ! функгцти) структурному преобразованию в теории регулировании соответствует ттекоторое пев.трожд(Ч1Т1ое irpoo6p;u{oB.mn(>