-2 1 О -1

Ъ = [1], c = [10j.

Построим для этой системы идентификатор первого порядка, динамика которого задана характеристическим многочленом фи (А.) = X -j- р.

Преобразуем матрицы системы к идентификационному

каноническому виду по формулам: /. = РЬ, с:= сР-1. Матрица Р = J

= РАР-\ Ъ В результате

Замечание, Подобные (и - 1)-мерные и вообще (п - /7)-мерные (где р - число линейно независимых выходов) асимптотические идентификаторы называют иногда идентификаторами Люенбергера, по имени американского ученого, впервые изучавшего их структуру. Q

В приведенном нами способе построения асимптотических идентификаторов входы ие играют какой-либо роли. Поэтому все наши рассуждения применимы к идентифицируемым системам с несколькими входами и одним выходом.

Алгоритм построеиия (я - 1)-мерного идевтвфвкато-

ра. Пусть заданы матрицы управляемой системы с одним выходом и, вообще говоря, многими входами (А, Ь, с}. Полученный нами алгоритм построения (п - 1)-мерного идентификатора состояния состоит из следующих шагов:

1. Матрицы системы {А, Ь, с} записываем в таком базисе, чтобы пара (А, с} имела каноническое идентификационное представление (ИКП).

2. Выбираем дин£й1ические свойства идентификатора - многочлен

3. Преобразуем] все матрицы системы с помощью матрицы Р вида (2). Уравнения искомого идентификатора имеют при этом вид

x{t) = Лх{1) + + btiO),

где Л - подматрица размеров ( - 1) X (тг -Л); расположенная в левом верхнем углу матрицы А, а - последний столбец матрицы А.

Пример 1. Рассмотрим полностью идентифицируемую систему второго порядка

расчетов получим 1

1 -2

с = [О 1].

Преобразуем теперь матрицы системы с помощью невырожденного преобразования (2)

РАР-* =

0 1 (1 + 8) [3(1-[3)-1 (3 - 2) J

РЪ =

о 1 1

-1

[О 1].

Окончательно уравнения идентификатора примут вид

li (t) = - (1 + Р) 1 (О + р (1 - Р) у (О + (О, *2 (О = у (О-

Структурная схема этого идентификатора приведена на рис. 26.1. Сравните эту схему со схемой идентификатора второго порядка, приведенной на рис. 25.4.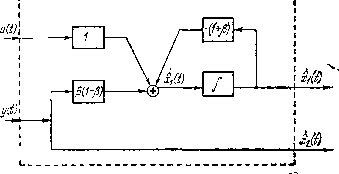

Рис. 26.1.

Идентификаторы Люенбергера для системы с многими выходами. Изучим вопрос конструирования асимптотических идентификаторов для идентифицируемых систем со многими выходами. Поскольку задача идентификации состояния дуальна задачам управления, мы можем при конструировании идентификатора состояния для системы с многими выходами использовать соображения, приведенные при решении задачи выбора обратной связи по

состоянию для системы с многими входами. Ясно, что из экономических соображений выгодно конструировать идентификаторы возможно меньшей размерности. Мы покажем, что если ранг матрицы С равен р, то асимптотический идентификатор состояния имеет размерность п ~ р и оценивает все переменные состояния системы. Эта задача будет решена в два этапа. Па первом этапе мы преобразуем уравнения системы в такую каноническую форму, ито новые уравнения можно рассматривать как сумму подсистем, каждая из которых имеет один выход. Затем для каждой из этих подсистем мы построим идентификатор, используя построенный выше алгоритм. Основу доказательства составляет выбор специального базиса в пространстве состояний.

Рассмотрим идентифицируемую систему (ЛС). Поскольку пара {А, С} идентифицируема, то пара {А\ С} управляема. Каноническое представление этой пары в пространстве состояний можно построить, воспользовавшись способом 2 выбора п линейно независимых векторов, приведенным в § 22. Обозначим через С; t-ю строку матрицы С {i =- 1, 2, . . ., р). Строки этой матрицы содержат по п элементов. Предположим, что эти строки линейно независимы. Воспользовавшись управляемостью пары {А, С} и применяя способ 2, найдем п линейно независимых строк вида

а,-1

Сх, ciA, ciA , . . ., ciA

Са, СзЛ, СаЛ, .

Ср, СрЛ, СрЛг.....СрЛР

Здесь -\- -г п. Построим из этих строк

(п X /г)-матрицу располагая строки в следующем порядке: Cl, CjA, CiA, . . ., Cg, сА, ... Тогда

Так как все строки в таблице (3) линейно независимы, то матрица Q неособенная и д1атрица Q существует.