288 Идентификаторы состояйий [гл. v

Обозначим столбцы матрицы следующим образом: = [eu, ei2,..., еца, eai, egg, . .esi, ..., вцл, ..., вр.].

Поскольку QQ~ = Е, то но определению выполняются следующие условия:

f 1, если i = I л j = q CiA%ii = \ (4)

I, 0 в противном случае.

Теперь примем в качестве базиса пространства состояний набор столбцов

[ei(ij, Лбцл, ...,А ei(ij, eijug,

Эти столбцы линейно независимы. Докажем сначала, что линейно независимы столбцы [eii., Ai, . . ., Л IcJ-Предположим, что существует нетривиальная линейная комбинация этих столбцов. Например,

deiy.. 4- ааЛе,. -)-... + а.а~%к = 0. Умножив это равенство слева на строку с, получим

{(XiCi + адЛ Н-----1- а1л.СЛ ) ецк = О,

но efi. 7 0. Значит, линейно зависимы строки набора (3) Полученное противоречие доказывает, что столбцы

ех1л., лецк,..., Л eifji.

линейно независимы при любом i = 1, 2, р. Вспоминая, что столбцы Cifi , 6214, . . ., epip линейно независимы по построению, легко видеть, что все столбцы набора (5) линейно независимы. Образуем из этих столбцов матрицу

Р~ = [eit, Aei,..., Л ер(хр]

и выберем столбцы этой матрицы в качестве базиса пространства состояний. Приведение матрицы С к этому базису в соответствии с формулой С: = СР~ приводит

К следующему виду уравнения наблюдения:

При вычислении С мы воспользовались формулой (4).

Б новом базисе уравнение х (t) = Ах (t) + Ви (t) примет следующий вид;

±21 i-32

0 *

0 *;

*

1 *:

*0 0 ... 0 *:

*i 1 0 . . . 0 *i *!0 0 ... 1 ♦!

x-h-Bu,

*! [0 0 ... 0 * *: ; 1 0 ... 0 *

. 0 0 ... 1 -

где знаком * обозначены, возможно, ненулевые элементы матрицы. Приведенную систему уравнений можно, очевидно, рассматривать как совокупность р систем уравнений, каждая из которых имеет много входов и единственный выход. Структурная схема полученного канонического представления приведена на рис. 26.2, Каждая из р систем имеет следующий вид:

-Ь D,y + BiU, (6)

Здесь Di и Bi ветственно.

г/ = [0 0. . . О Их матрицы размеров р.; X /? и р X m соот-

10 Ю. и Андреев

Используя полученное каноническое представление, можно непосредственно применить к системе с многими выходами результаты, полученные при построении идентификаторов для системы с одним выходом. Для каждой подсистемы (6) можно построить асимптотический идентификатор размерности р; - 1. Следовательно, размерность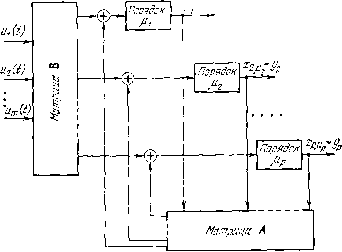

Рис. 26.2.

идентификатора системы равна сумме размерностей р идентификаторов для систем (6):

2(Pi -1) = /г--/).

Эти Идентификаторы дают на своих выходах п - р оценок переменных состояния. Выходной вектор системы доставляет еще р оценок. Характеристический многочлен каждого из р идентификаторов согласно доказанному ранее результату (теорема 1) можно выбирать по своему усмотрению. Единственное ограничение, связанное с реализуемостью системы, состоит е том, что этот многочлен должен иметь действительные коэффициенты. Поэтому, если ком-