ИДЕНТИФИКАТОРЫ состояния

[гл. V

Рассмотрим теперь задачу конструирования идентификатора {п - 1)-го порядка для системы х {t) = Ак (t), у {t) = сх (f), где {А. с} представлены в виде (ИКП).

Если уравнения идентификатора имеют вид

00...

1 о ... -р.

0 О ... -р.

z(t)

-о . . 3 (а-р)-а

то решением уравнения ТА - DT = S будет матрица

1 О ... О -

0 о . . . 1 -

размеров (п - 1) X п.. В этом случае оценки переменных £г получаются из переменных Zi по следуюп1;им формулам:

Поскольку коэффициенты можно выбирать но своему усмотрению, то динамические свойства идентификатора по-прежнему могут назначаться произвольно. В общем случае, условие идентифицируемости системы гарантирует существование матриц D (с произвольно заданным харан-теристическим многочленом) и Г, Q, удовлетворяющих уравнение ТА - DT QC та таких, что выходы идентит фикатора % [i) дают оценки всех компонентов вектора со стояний. Рассмотренный подход позволяет, таким обра-зом, выяснить алгебраическую сторону проблемы конструи рования идентификатора.

Пример 2, Пусть матрицы системы имеют вид:

-2 1-

с = [1 Oj.

Выберем собствелное значение идентификатора А, = -3. Тогда уравнение идентификатора пмеет вид

2(0--=-Зз(0 + [1 0]

ж1 {t

u{t).

Пусть Z [t) = Tx {t), где Т является решением уравнения Решение этого уравнения имеет вид Т =

числим ГЬ

. Вы-

=--Окончательно уравне-

ние идентификатора получим в виде и

z{t)x,{t)~-x.,{t).

Структурная схема данной системы и построенного идентификатора приведена на рис. 26.3.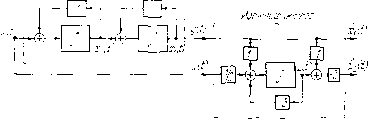

Рпс. 26.3.

Еще один сиособ построения {гг - р)-мериого идентификатора. Пусть в уравнениях (ЛС) в условиях теоремы 2 матрица С имеет ранг р. Выберем в качестве новых переменных состояния р линейных комбинаций компонент вектора х (), задаваемых уравнением наблюдения системы, и еп],е {п - р) линейно независимых комбинаций компонент X (t), заданных равенством z {t) = Lx {t), где

L - матрица (г* - р) X п, строки которой ливойпо независимы. Проведенную замену переме1П1ых можно записать так:

K{t) = Px{t).

(12)

В соответствии с выбором L это - невырожденная замена переменной, и матрица Р имеет обратную. Поэтому

Подставляя новые переменные в уравнения системы, получим

у {0-1

= РАР

-lit)

-hPBaitl

или, разбивая матрицы PAP и РВ на блоки, имеем

и(0. (*)

Из этого представления следует, что уравнение для переменных Z (t) имеет вид

i{t) = a z{t) + Ay{t)B,u{t)-

Возьмем в качестве уравнения оценки вектора z [t] уравнение

Z (О aJ (t) Jr А,уУ {t) + В,а (О, Z (0) 0. (13)

Тогда ошибка оценки z {t) = z (t) - z (t), как нетрудно видеть, удовлетворяет уравнению

z(0 = Azit), z(0) = z(0)-z(O).

Если матрица A устойчива, то ъ {t)О ири t-oo. Таким образом, оценка вектора состояния системы (ЛС) определена равенством

x(t)p- 1-.-