§ 27. Конструкция регуляторов

В главе IV было показано, что управляемой стационарной системе с помощью обратной связи можно придать произвольные динамические свойства. Именно, корни характеристического уравнения такой замкнутой системы можно выбирать произвольно. Эти неограниченные возможности стационарной обратной связи нельзя, вообще говоря, использовать из-за того, что не все компоненты вектора состояний обычно доступны для измерения.

В главе V выяснено, что для идентифицируемой системы можно построить динамическую систему (идентификатор), выходные переменные которой асимптотически прибли /каются к переменным состояния исходной системы.

Теперь предстоит объединить эти результаты в конструкции одного регулятора.

Этот регулятор состоит из динамической системы, вырабатывающей на своем выходе оценку вектора состояний X {t) по результатам измерения выхода системы у [t) и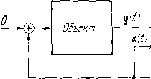

Идеитифи -натр

СОСТЮЯН.Я

обрашая

Рис. 27.1.

входа U (i), и из стационарной обратной связи вида и {%) =

= - К± (О (рис. 27.1)

Применение /г-мерных идентификаторов. Рассмотрим п-мерную управляемую и идентифицируемую линейную систему

х(0 - A%{i) -t- Bu{t), y(t)CK{t).

(ЛС)

Пусть, матрица обратной связи К выбрана так, что характеристический многочлен матрицы [А - ВК] совпадает с выбранным нами н;елаемым многочленом сру (X).

Предположим теперь, чт о построен асимптотический идентификатор состояния, уравнение которого имеет вид

x (t) = U - Ш X (t) 4- Ху (t) + Ва (1); (И)

обозначим характеристический многочлен идентификатора фи (А.) = Ц>[А-ьс}- Так как вектор х (t) недоступен для измерения, то попробуем заменить в цепи обратной связи вектор X {t) на его оценку х (t). Напомним, что поскольку многочлен фи (Я) можно выбрать по своему усмотрению, то всегда можно получить произвольную динамику стремления оценки X (i) к X (t) при tоо. При такой замене основной интерес представляет два вопроса: (1) матрица К выбрана в предполо;кении. что известно состояние X (t), а потом вектор состояпия замепеп его оценкой х {t). Получится ли прежний результат? Другими словами, будет ли система с обратной связью по-прежнему иметь желаемый характеристический многочлен фу (Я)? (2) Какой эффект вносит в систему идентификатор? Какое отношение к характеристическому многочлену замкнутой системы 2л-го порядка будет иметь характеристический многочлен идентификатора? Войдут ли собственные числа идентификатора в замкнутую систему без изменений? Оказывается, что выбранные характеристические числа системы с обратной связью по состоянию и характеристические числа идентификатора войдут в замкнутую систему без изменений. Именно, справедлива следующая

Теорема 1. Пусть дана управляемая и идентифицируемая система {А, В, С). Пусть матрица К выбрана так, что характеристический многочлен матрицы [А -

- ВК] совпадает с заданным многочленом фу (к) -- X + Н Vit -- . . . 4 пусть выбрана матрица L такая, что характеристический многочлен матрицы [А -

- LC] совпадает с фи [Ц =-- + + - . - К, тогда характеристический многочлен замкнутой системы 2п-го порядка

x{t) = Ax{t) - BKx{t),

X (t) - [А - LC] X (t) - ВКх (t) 4- LCx (t),

который мы обозначим через фо (к), совпадает с произведением выбранных многочленое фо (к) Цу (Я)-фи (Я).

Доказательство. Вычислим характеристический многочлен получившейся системы 2й-го порядка

Л \ВК

lcia- ic - BK

Сделаем певырождепную замену переменной х (t) = X (i) - X (f). Матрица этого преобразования имеет вид

где Е - единичная матрица размеров п X /г. Б новых координатах матрица замкнутой системы будет клеточпо-диагональной матрицей

Характеристический многочлен этой клеточно-диагопаль-ной матрицы совпадает с произведением характеристических многочленов клеток, стоящих на диагонали. Именно, Фо (К) фу (?)-фи О

Доказанная теорема очень важна для приложений. Она утверждает, что поскольку речь идет о характеристических числах замкнутой системы, то в некоторолг смысле пет разницы между использованием в цепи обратной связи вектора X (t) и вектора х {t). Следовательно, и это особенно важно и удобно, конструирование цепи обратной связи и конструирование идентификатора можно осуществ;гять независимо. Характеристический многочлен замкнутой системы будет равен произведению характеристических многочленов системы с обратной связью но состоянию и идентификатора. При конструировании обратной связи мы имеем дело с двумя независимыми задачами, каждая из которых л-мерпа.

Для случая, когда управляемая и идентифицируемая система имеет единственный вход и один выход, формулы построения -мерной обратной связи, обеспечивающей заданный набор 2п собственных значений матрицы замкнутой системы, можно представить в замкнутой компактной форме.