сдвинутой импульсной характеристики (рис. 2.3, б). Полный сигнал в момент времени (рис. 2.3, в) равен интегралу:

- оо

называемому интегралом суперпозиции. В него входят три времени: время входного сигнала ti, время выходного сигнала и время памяти системы t2-ti. Интегрирование ведется по значениям t2 <ti, т. к. h{t2 -t]) = О при отрицательных значениях аргумента. Другими словами, реализуемая система помнит прошлое, но не знает будущего.

Интеграл суперпозиции словесно можно сформулировать так: величина выходного сигнала в настоящий момент равна взвешенному интегралу от входного сигнала за прошлое время, причем весовым коэффициентом является импульсная характеристика, играющая роль памяти системы. *

Введя обозначения: t2-ti = T и (2= получим:

V,(/)=]/z(T)V,(/-T)Jr- [2-4.2]

Можно также использовать другую форму записи:

v,(t)=]vXT)h{tr)dT- [2.4.3]

Обе записи с точностью до одного из пределов соответствуют обычной формуле свертки с учетом физической реализуемости системы - значение выходного сигнала системы в момент времени / не может зависеть от сигналов, поступивших на её вход после этого момента. Для реализуемой системы интегрирование нужно вести по времени памяти системы в пределах от О до оо; при интегрировании по времени прихода входного сигнала интегрирование ведется от - оо до Г.

Приведем ещё одну графическую интерпретацию интеграла суперпозиции. Как уже отмечалось, импульсная характеристика (рис. 2.4, а) входит в интеграл суперпозиции как функция памяти h(t2 - tf). Можно изобразить функцию памяти в зависимости от при ti в качестве параметра (рис. 2.4, б), или рассматривать h{t2-ti)

как функцию времени входного сигнала параметра (рис. 2.4, в).

h(t) h(t2-ti)

ti при t2 В качестве

h(t2-t,)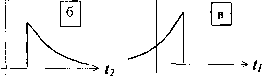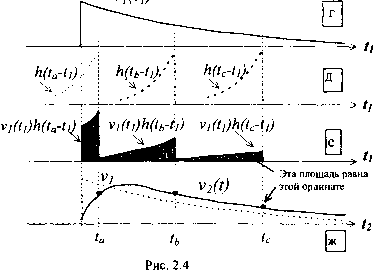

Мы воспользуемся последним вариантом. Умножим входной сигнал (рис. 2.4, г) на функцию памяти (рис. 2.4, д) и получим взвешенный входной сигнал (рис. 2.4, е).

Площадь, ограниченная взвешенной кривой и осью времени входного сигнала, равна значению выходного сигнала (рис. 2.4, ж) в заданные моменты времени (рис. 2.4, г) для выходного сигнала ta, tb и tc. Если рассматривать умножение и интегрирование по времени как одновременные операции, то можно вообразить, что функция памяти скользит по временной функции входного сигнала.

порождая при этом последовательные мгновенные значения выходного сигнала.

Интеграл суперпозиции позволяет дать точное условие устойчивости. В устойчивой системе выходной сигнал имеет конечное значение при всех конечных входных сигналах, т. е. при \Vi(t)\ < М, где М- положительное действительное конечное число. Откуда вытекает необходимое и достаточное условие устойчивости:

V{t)\< М j\h(T )\dT [2-4.4]

т. е. система устойчива, если её импульсная характеристика абсолютно интегрируема:

1h{t)\dt<oo- [2-4.5]

2.5. Интеграл суперпозиции как корреляционная операция

Введенное в этом разделе понятие функция памяти применительно к импульсной характеристике с аргументом (г - tj) требует некоторого уточнения. Поскольку память обращена к прошлому, то естественно связать функцию памяти с величиной выходного сигнала в настоящий момент времени, возникшего в ответ на единичный импульс, поданный на вход t секунд назад. При таком определении функция памяти

m(t) = h(-t). [2.5.1]

Подставляя это равенство в [2.4.Ъ], получаем:

- 00

По существу, всякая линейная система передачи является коррелятором, выходной сигнал которого в каждый момент времени определяется степенью корреляции прошлого входного сигнала с функцией памяти.

К интегралу суперпозиции, как частному случаю операции свертки, применимы законы: