Тогда ФНЗС

где A/- девиация частоты.

Диаграмма неопределенности радиоимпульса с ЛЧМ (рис. 4.3) представляет собой также эллипс, но повернутый на угол aarctgAjT/т ,

причем при изменении угла а крайние правая и левая горизонтальные точки ПГТ и ЛГТ перемещаются по вертикальным прямым. Площадь эллипса по-прежнему не меняется, но за счет растяжения по большей оси эллипс сжимается в поперечном направлении. Протяженность ДН по горизонтали уменьшается, что соответствует сжатию импульса с ЛЧМ при оптимальной его обработке. Рис. 4.3. Диаграммы пеопределеиности пря- Если ИСПОЛЬЗОВать внутри-

:ХГ ГсЗл 7 * * импульснук, фазокодовук, мо-

ляцию псевдослучайным кодом, то тело неопределенности будет состоять из главного пика (острия) и достаточно тонкого пьедестала ( шляпки ), образуя кнопкообразную ФНЗС (см. рис. 4.18).

Пример. Построим ДН радиоимпульса с гауссовской огибающей для т = 1 мкс и т = 5 мкс, приняв с = 0,5.

Решение. Учитывая, что yj-2\n{c) = J-2\n(0,5) = 1,177, запишем уравнение ДН в виде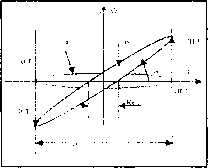

(1,177г,.) (0,374/г )2

Для построения ДН воспользуемся параметрической формой уравнения эллипса:

х = аcos(), у = аsin(), Q<(p<2n ,

где = 0;-0,01,...,2я.

Для короткого импульса Ti=1mkc, 1=1,177 Ti, 6=0,374ti, Х\ =а\ cos(), Fi =b\ sin();

Для длинного импульса Т2=5мкс, а2 1Л77т2, 2=0,374x2, aj cos(), Y2 =2 s\x\{(p).

Результаты решения представлены на рис. 4.4.

0.5т

-0.5 -

У2(Ф)

0.5т

-0.25--

-0.5- Х2(Ф)

--э-~-б

Рис. 4.4. Диаграммы иеопределсипости короткого (1мкс) и длинного (5мкс) импульсов

Пример. Построить ФНЗС и ДН радиоимпульса с прямоугольной огибающей при т =1 мкс.

Решение. т =1 мкс, Af= 1/т , расчет проведен в пятидесяти точках.

я Ft..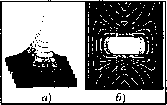

Результаты решения представлены на рис. 4.5.

В табл. 4.1 приведены примеры оди- ,(1*

ночных сигналов, их спектров и ДНЗС.

Таблица 4.1

Сигнал

Спектр

£7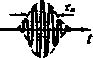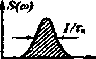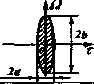

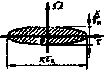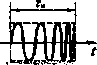Функции неопределенности повторяющихся сигналов. Функция повторяемости сигнала (рис. 4.6) задается в виде последовательности 5-функций:

f/2(0=;5(/-/?;),

/ =-<

где Т - период повторения.

Функция повторяемости ДКФ:

(4.10)

Рассмотрим ФН и ДН сигнала в виде бесконечной последовательности 5-функций следующих с периодом повторения 7п=1 мс. Пусть одиночному Ux{t) соответствует ДКФ R, Xx,F), тогда ДКФ fmziyj) повторяющегося в бесконечных пределах сигнала U\(t)

Рис. 4.6. ФНЗС (а) и ДН (б) функции повторяемости МОЖНО наЙТИ С ПОМОЩЬЮ

сигналов интеграла свертки: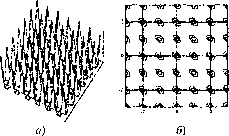