На рис. 4.13 приведена схема усилителя с обратной связью, в ней 1/2= [t/i + /Co.c(ici))t;2]Ky(i(i)), а поэтому комплексный коэффициент передачи схемы с обратной связью

Ку (i (й)

K(ia)) = =-

Ui l-f-K.c(i >)/Cy(i >)

(4.56)

При ui = 0 (короткое замыкание на входе) схема рис. 4.13 сводится к схеме рис. 4.3 и произведение /Со.с(1и) Ку(1и) равно коэффициенту передачи напряжения по замкнутой цепи генератора

рис. 4.3 или 4.9а. Обозначим Ky(icu) =/Су(а))е у , Ko.c(i<o) = =/Co.c(ia))e о-с . Тогда условие пересечения годографом оси абсцисс при К<1 можно записать в виде двух условий: условия баланса фаз

фу(сй)-1-фо.с(сй)=2л;п, где п=0, I, 2,

(4.57)

передачи

(4.58)

определяющего частоту ©о, на которой коэффициент К (ico) становится действительным, и амплитудного условия

Ку1{ао) Ко.с (соо) = /С (©oX.l -

Самовозбуждение колебаний в усилителе происходит, если при соблюдении условия баланса фаз (4.57) знак неравенства в (4.58) меняется на обратный.

Для иллюстрации критерия Найквиста рассмотрим определение условий самовозбуждения генератора рис. 4.16. Размыкая схему в точках, обозначенных крестиками, и принимая Zi,x = oo, получим эквивалентную схему рис. 4.14а. Считаем схему для малых амплитуд напряжения в линейной с крутизной S в рабочей точке и пренебрегаем влиянием напряжения на контуре на ток 1; тогда комплексная амплитуда его первой гармоники /к1=517в.

- +

Рис. 4.14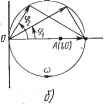

Напряжение на контуре на любой частоте f/к =/ш Zg = в

2 Д(в

гдел;С-- обобщенная расстройка контура. Выходное напряжение

Овы=ЮкМ1Ь. Комплексный коэффициент передачи схемы рис 4 14а равен

K(icu) =

i (1 -1- i I)

(4.59)

Из (4.59) получаем выражения фазовой и частотной характеристик:

Ф=-arctgl, (4.60)

Ш8Яа MSRg

Здесь Ko=(WL)Si?3 -коэффициент передачи при ф=0, т. е. на частоте, равной резонансной частоте контура Юо.

Построение амплитудно-фазовой характеристики разомкнутой цепи иллюстрирует рис. 4.146. Задаваясь различными значениями частоты ю, из .(4.60) получаем ф, а затем согласно (4.61) определяем К как проекцию вектора Ко на линию, идущую под углом ф к оси абсцисс. Линия, прочерчиваемая концом вектора K(iu)), при изменении ю от О до оо и будет АФХ. В рассматриваемом, случае она проходит через вершины прямоугольных треугольников, а потому оказывается окружностью диаметра Ко- По критерию Найквиста условие самовозбуждения генератора будет Ко>0 или с учетом (4.61) M><L/SRa, что совпа- дает с .условием самовозбуждения (4.13), полученным из решения дифференциального уравнения генератора. Частоту (в возникающих колебаний определим, приравнивая нулю (4.60): сй=;(Вй=1/VC.

Критерий Найквиста широко используется при оценке устойчивости усилителей и других устройств. Достоинством его является то, что он не требует составления подчас весьма сложных дифференциальных уравнений исследуемых устройств, а оперирует с частотными и фазовыми характеристиками отдельных звеньев системы, почти всегда определяемыми расчетным или экспериментальным путем при проектировании каждого устройства. В то же время он является менее общим, чем критерий Михайлова, так как оказывается непригодным в случае неустойчивой разомкнутой цепи, а также тогда, когда порядок дифференциального уравнения разомкнутой цепи выше, чем замкнутой.

УСТОЙЧИВОСТЬ СОСТОЯНИИ РАВНОВЕСИЯ по ЛЯПУНОВУ

Классический метод определения устойчивости был разработан в конце XIX в. выдающимся русским математиком М. А. Ляпуновым и с тех пор носит его имя. Определение устойчивости по Ляпунову состоит в следующем: состояние равновесия является устойчивым, если при любой заданной области е допустимых отклонений от состояния равновесия (например, область е вокруг точки равновесия О на рис. 4.15) можно указать область 6(8), окружающую состояние равновесия и обладающую тем свойством, что ни одно движение, начинающееся внутри б(е), никогда не достигнет границ области е. Иными словами, устойчивое состояние равновесия характеризуется тем, что отклонение от этого состояния не превысит сколь угодно малой величины, если начальное возмущение достаточно мало. Если же возникающее малое отклонение с течением времени затухает, то такое состояние равновесия называется асимптотически устойчивым. Следовательно, если малые начальные отклонения приводят к возникновению достаточно малых периодических колебаний в системе, состояние равновесия считается устойчивым, но не асимптотически.

М. А. Ляпунов обосновал метод аналитического исследования устойчивости состояния равновесия нелинейных цепей, заключающийся в замене характеристики нелинейного элемента касательной к ней, взятой вблизи исследуемого состояния. Рассмотрим метод Ляпунова для систем, описываемых нелинейными диф-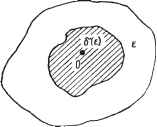

Рис. 4.15

ференциальными уравнениями первого и второго порядка. Пусть некоторая система описывается нелинейным дифференциальным уравнением первого порядка

dx/dt=f{x), (4.62)

где X может быть током, напряжением, зарядом. Состояниям равновесия системы соответствуют значения х===Хо, для которых dx/dt=0, или

/(хо).=0. (4.63)

Для исследования устойчивости этих состояний будем считать

хХо+Ах, (4.64)

где Ал; - малое отклонение от состояния равновесия. Подставляя (4.64) в (4.62), получаем

dAx/dt=f(xo+Ax), (4.65)

поскольку хо - величина постоянная. Правую часть (4.65) раскладываем в ряд Тейлора

fixo+Ax) =(f(хо) +Ах Г{хо) +(>(хо) +...

(4.66.)

Согласно Ляпунову ввиду малости Ал; ограничиваемся в выражении (4.66) первыми двумя слагаемыми. Подставляя их в (4.65), получаем с учетом (4.63) линейное уравнение первого приближения - уравнение вариаций:

dAxfdt=f{xo)Ax. (4.67)

Обозначив /(хо)=а, получим решение этого уравнения:

Ах=.Се *. (4.68)

где С - постоянная интегрирования.

Если а>0, т. е. производная df/dx при х=Хо> положительна- Ал; будет нарастать, т. е. состояние равновесия окажется неустой-136