чивым. Если же а<0, то состояние равновесия при хХо будет устойчивым. На рис. 4.16 построен трафик функции f(x), для которой равновесие имеет место в точках Хои Хо2, лгоз- Остальные значения х изменяются во времени согласно (4.62): возрастают, если f(x)>0, и уменьшаются, если f(x)<0. Направления изменения координаты X отмечены стрелками. Из рис. 4.16 и выражения (4.68) следует, что состояния равновесия: Хо2 - устойчивое, Xoi и Хоз - неустойчивые.

Переходим к рассмотрению системы, описываемой нелинейными дифференциальными уравнениями второго порядка или двумя уравнениями первого:

- = Р(х, у) и =Q{x, у). (4.69)

at at

Состояния равновесия системы определяются координатами точек Хо, уо, в которых производные dx/dt=0 и dy/dt = 0 или

Р {хо, о) = о и Q {хо, Уо) = 0. (4.70)

Дадим X и у небольшие начальные отклонения от Хо и уо:

х=Хо+Ах и у-=Уо+Ау. .(4.71)

Подставляем (4.71) в (4.69) и раскладываем правые части в ряд Тейлора

Р{хо + Ах, уо+Ау) =Р{Хо,Уо) +АхРх(хо, Уо) +

+АуРу{Хо, Уо)+... = Q(хо+Ах, уо+Ау) =Q{Хо, Уо) +AxQ{xo, уо) +

,(4.72)

-\-AyQy{Xo, Уо)+-

Здесь {Хо, Уо) = {дР/дх)х , у,; Ру {хо, уо) = {dPIdy) ;

Qx {Хо. У1) = {dQIdx)у ; Qy {хо, Уо) = {dQ/dy) у .

Пренебрегая в (4.72) слагаемыми, имеющими множители Ах и Ау в степенях выше первой (т. е. нелинейными членами), и принимая во внимание (4.70), получаем два линейных уравнения вариаций:

=Р.{хо, уо)Ах+Ру{Хо, уо)Ау,

=Qx{Xo, yo)Ax+Qy{xo, уо)Ау, dt

(4.73)

которые после несложных преобразований сводятся к одному линейному уравнению второго порядка относительно Ах

-P+Q) + ipQ-PQ)Дх = о (4.74)

dt dt

или такого же относительно Ау.

Переписав это уравнение в виде

dhx , д л

(4.75)

где ао=1, ai=-{Px+Qv), a2-=PxQy-PyQx, мы можем для оценки устойчивости состояния равновесия использовать критерий Рауса - Гурвица.

Для иллюстрации метода Ляпунова рассмотрим вопрос об устойчивости состояний равновесия генератора на туннельном диоде. Принципиальная схема такого генератора для достаточно высоких частот (рис. 4.17а) состоит из туннельного диода ТД, индуктивности Lh, используемой для настройки

+0-й-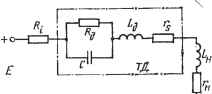

Рис. 4.17

генератора, сопротивления нагрузки и источника питания Е. Переходя к расчету генератора, учтем, что источник питания Е обладает некоторым внутренним сопротивлением Ru а туннельный диод заменим эквивалентной схемой (рис. 4.176), содержащей - нелинейное сопротивление р-я-перехода (его вольт-амперная характеристика 1=Ф(и) приведена на рис. 4.18а), С -емкость р-я-перехода , £-д - индуктивность выводов, Гв - сопротивление объема полупроводника, примыкающего с обеих сторон к р-я-переходу.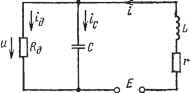

Рис. 4.18

Приняв 7-=i?i+s-l-rH И Е=Ец+Еш, получаем эквивалентную схему генератора на ТД (рис. 4.186). С учетом обозначений рис. 4.186 составим уравнения:

откуда

Lr.+L(di/dty+u==E, i=iR+ic, 1д=Ф( ). ic = C(du/dt),

С{du/dt) = i-Ф(и), L{di/dt) = E-u-ir.

(4.76)

-(4.77), (4.78)

Величина емкости ТД также несколько зависит от напряжения. В последующем для упрощения анализа считаем С постоянной.

Исключая из (4.77) и (4.78) одну переменную, получим нелинейное уравнение генератора на ТД

du ,1 . £

Ф ( )

+ -77Г[ + -Ф(и)] = 77Г, (4.79)

dt LC LG

в котором W{u)=dO(u)/du. В состоянии равновесия du/dt=0 и di/dt~0, а потому согласно (4.77) и (4.78)

1=Ф( ), i=(E-u)fr. (4.80)

Токи io и напряжения о, соответствующие возможным состояниям равновесия системы, должны удовлетворять обоим соотношениям, поэтому они могут быть определены, как показано на рис. 4.18й, по точкам пересечения характеристик (4.80). В общем случае получаем три состояния равновесия: в двух (точках В н С) нелинейный э.пемент обладает положительным дифференциальным сопротивлением, в одном (точка А) - отрицательным. Для оценки устойчивости этих состояний подставляем ы= о+Аи и i=io+Ai в (4.77) и (4.78), считая, что Uo и to удовлетворяют (4.80). Ограничиваясь в разложении Ф( о+А ) для Дгг<Ыо первыми двумя слагаемыми O(wo+Aw) =Ф(ио)+Д Ф(ио), получим

Д1 = С--+ ДиФ(Ио). (4.81) dt

L --- +Д u-\-r Д 1=0. (4.82) dt

Коэффициент Ф{ио) = \/Яа является величиной, обратной дифференциальному сопротивлению нелинейного элемента в рабочей точке. Из (4.81) и (4.82) получаем уравнение вариаций

й-Ды / г . 1 \dAu . 1

Уравнение (4.83) аналогично (4.75), причем

(4.83)

(4.. 4)

Согласно критерию Рауса - Гурвица состояние равновесия при ао>0 является устойчивым, если

ai>0 и а2>0. (4.а5)

Состояния равновесия, соответствующие точкам В к С, являются устойчивыми, так как в них /?д>0 и условия (4.85) выполняются. Для определения устойчивости состояния равновесия в точке Л, где ?д<0, удобно обозначить

J? =-i? (4.86)

и переписать условия (4.85) в виде

7-C/L-1/./? >0, 1-7-/.?д>0. (4.87), (4.88) Условие (4.88) означает

г<Ш. (4.89)

Соотношение (4.89) называют условием устойчивости по постоянному току, так как его выполнение гарантирует сохранение рабочей точки на падающем участке, а нарушение приводит к переходу к другому состоянию равновесия. Таким образом, для того чтобы рабочая точка находилась на падающем участке ГД, питание схемы необходимо осуществлять от источника напряжения, обладающего малым внутренним сопротивлением Ri.

Для переменного тока схема рис. 4.186 представляет параллельный колебательный контур с эквивалентным сопротивлением Ra=L/Cr, подключенный к нелинейному сопротивлению ? . Перепишем (4.83) в виде

+-l/-i- -L + J-fl-)Д. = 0. (4.90)

С\ Ra (;?д J dt LC\ (/?д1 /