Условие устойчивости (4.87) можно записать как

/?э< . (4.9-1)

Из уравнения (4.90) следует, что при выполнении условия устойчивости (4.89) колебания в генераторе затухают, если коэффициент при dAu/dt положительный, и нарастают, если отрицательный. Неравенство (4.91) является условием предотвращения нарастания колебаний в точке А, поэтому его называют условием устойчивости по переменному току.

В усилителях на ТД требуется обеспечить устойчивость состояния равновесия на падающем участке, т. е. выполнить условия устойчивости и по постоянному и по переменному токам. В генераторах нужно выполнить условие устойчивости по постоянному току (для того, чтобы рабочая точка находилась на падающем участке) и нарушить условие устойчивости по переменному току, тогда возникающее из-за действия флуктуации колебание небольшой амплитуды будет нарастать.

Рассматривавшиеся до сих пор методы анализа и критерии устойчивости нелинейных устройств основываются на использовании укороченных линейных уравнений первого приближения [смотрите например, переход от уравнения (4.66) к (4.67)]. Возникает естественный вопрос, в каких случаях результат исследования устойчивости с помощью линеаризованных уравнений вариаций совпадает с результатами такого же исследования исходной нелинейной системы. М. А. Ляпуновым было доказано, что это имеет место в случаях, когда решение линеаризованных уравнений возмущения асимптотически устойчиво или неустойчиво. Если же решение линеаризованных уравнений приводит к устойчивости неасимптотической (например, к малым незатухающим колебаниям около состояния равновесия), для нелинейной системы такое решение может оказаться неверным, поскольку отбрасываемые при линеаризации выражений (4.66), (4.72) и других нелинейные члены высшего порядка малости приобретают теперь решающее значение.

Подтвердим сказанное примером. Пусть уравнения вариаций системы второго порядка имеют вид

= - а I/ -f- алгУМ. -=ах+ау VTF, (4.92), (4.98.) dt dt

где а=const. Будем рассматривать движение на плоскости х, у. Обозначим /= -расстояние до начала координат. Умножая (4.92) на х, а (4.93)

на I/ и складывая их почленно, получим уравнение drldt=a.r. Разделяя переменные и интегрируя от U до t, полагая, что при этом расстояние изменяется от Го до г, получим

r=rol[\-aro(t-U)]. (4.94)

При а<0 и t-oo г->-0, что соответствует асимптотической устойчивости; при а>0 и t-to+1/аго r-foo, что означает неустойчивость состояния равновесия.

Если же линеаризовать правые части уравнений (4.92) и (4.93), получим dx dy dx

--=- 1/, - =ах или- +ах=0. Корни соответствующего характеристиче-

dt dt dt

ского уравнения будут мнимыми (как для колебательного контура без потерь), что означает существование колебаний с постоянной амплитудой г= =const, т. е. неасимптотическую устойчивость состояния равновесия. Как видим, в данном случае анализ устойчивости.состояния равновесия нелинейной системы по линейным уравнениям первого приближения приводит к неверным результатам.

ПРЯМОЙ МЕТОД ЛЯПУНОВА

М. А. Ляпуновым был предложен и другой метод анализа устойчивости состояния равновесия нелинейных систем, называемый прямым или вторым методом Ляпунова. Этот метод основан на формировании и рассмотрении специальных функций V(x, у), где X и у--небольшие отклонения (вариации) переменных от состояния равновесия, соответствующего л:=0 и у=0. Требования к функции V(x, у):

в некоторой области, окружающей начало координат, V(x, у) непрерывна вместе со всеми частными производными первого порядка;

в начале координат F(0,0) =0;

во всех остальных точках этой области V(x, у) отличается от нуля и принимает значения одного знака.

Функция V(x, у), обладающая такими свойствами, называется знакоопределенной: определенно-положительной или определенно-отрицательной. Функцию называют знакопостоянной (положительной или отрицательной), если она также сохраняет в области постоянство знака, однако нулевые значения имеет не только в начале координат. Эти функции называют функциями Ляпунова.

Рассмотрим некоторые функции V(x, у). Функция

У==х-Л-у\ (4.95)

построенная на рис. 4.19а, является знакоопределенной (определенно-положительной): в точке равновесия У(0, 0)=0, а в любых других точках У>0. Функция V=x-2ху-\-у=(х-уу, построенная на рис. 4.196, .знакопостоянна (положительна), но не знакоопределенна, так как У==0 не только в начале координат, но и в точках, где х=у; при иных значениях X и у У>0.

Обращаясь к знакооп-ределенным функциям, например к (4.95), можно заметить, что кривые V{x, у)=С, где С -фиксированный параметр, являются замкнутыми кривыми, охватывающими начало координат, причем

кривые с меньшими С располагаются ближе к началу координат. Используя эту особенность У-функций, М. А. Ляпунов доказал теоремы [8]..

Теорема 1. Если дифференциальные уравнения возмущенного движения таковы, что можно найти знакоопределенную функцию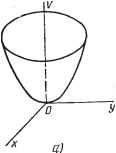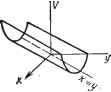

Рис. 4.19

Здесь изложение ведется для системы второго порядка, характеризующейся двумя независимыми переменными х v. у, хотя метод применим для систем любого порядка.

V(x, у), производная которой dV/dx была бы знакопостоянной функцией противоположного с V знака или тождественно равна нулю-, то равновесие системы в начале координат устойчиво.

Теорема 2. Если же производная dV/dx Является знакоопреде-ленной функцией противоположного с V знака, то равновесие системы в начале координат асимптотически устойчиво.

Для иллюстрации этих теорем на рис. 4.20 построено несколько замкнутых кривых определенно-положительной функции

V{x, у) =С для значений Ci<i <С2<Сз. Аргументами функции V{x, у) являются отклонения х и у от состояния равновесия, которые изменяются во времени в соответствии с характером возмущенного движения. Поэтому и значения функций V[x{t), y{t)] и ее производной dV/dt также изменяются во временц. Пусть производная dV/dt знакоопределенна и имеет противоположный с V знак, для рис. 4.20 она определенно-отрицательна (dV/dt<CO). Если в начальный момент to У-функция имела значение Уо=Сз, то за время t-io она изменится на величину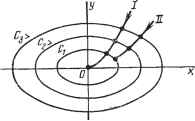

Рис. 4.20

- -if

>(4.96)

Очевидно, 1/<1/о = Сз. В рассматриваемых условиях с течением времени функция V последовательно проходит через значения Сз, Сг, Ci и вместе со своими компонентами хну приближается к началу координат (линия 1 на рис. 4.20), что означает асимптотическую устойчивость состояния равновесия.

Если же функция dV/dt в рассматриваемом случае знакопостоянна (отрицательна), то в процессе уменьшения V, происходящем согласно (4.96), она может достичь значения V=Vi, при котором dV/dt=0 при Х1ФО. Тогда дальнейшее уменьшение V функции, т. е. приближение к состоянию равновесия приостановится. Этому соответствует неасимптотическая устойчивость состояния равновесия и линия на рис. 4.20.

Прямой метод Ляпунова является исключительно эффективным методом исследования устойчивости состояния равновесия нелинейных систем. Основной трудностью на пути его использования является отсутствие общего метода построения функций Ляпунова, хотя существует ряд приемов, пригодных для уравнений вариаций определенного типа.

Пример. Пусть возмущенное движение описывается уравнениями

dx/dt=y~Qx\ dy/dt=-x5y (4.97)