Для построения фазовых траекторий, т. е. зависимости у{х), нужно из уравнений (4.185) исключить время. Деля одно из этих уравнений на другое, получаем уравнение фазовых траекторий в дифференциальной форме:

dy/dxQix, у)1Р{х, у). (4.191)

Уравнение фазовой траектории у(х) может быть получено в результате интегрирования (4.191). Аналитически это удается сделать лишь в простейших случаях (см. ниже пример LC-контура без потерь). В большинстве случаев переменные в (4.191) не разделяются и расчет фазовых траекторий следует осуществлять численными методами на ЭВМ. Известны и графические методы расчета и построения фазовых траекторий: метод изоклин, дельта-метод, метод Льенара и др. [24, 2].

При построении фазовых траекторий нередко используются изоклины-ш-НИН, во всех точках которых угол наклона а касательной к фазовой траектории одинаков. Уравнение изоклины

dx - Рх.у) -

где ft=tg а. Уравнение изоклины вертикальных касательных получается из (4.192) при й=оо;

Р(х,у)=0. (4.193)

Уравнение изоклины горизонтальных касательных получается из (4.192) при А=0;

Q(x,y)={). (4.194)

Если исходными уравнениями считаются (4.187) или (4.186), то согласно (4.188) и (4.193) касательные к фазовым траекториям будут вертикальными иа оси абсцисс (г/=0), горизонтальными на линии у=-\х1Ф{х). Записав первое из уравнений (4.187) в виде dx=ydt, убеждаемся в том, что в этом случае в верхней полуплоскости (у>0) изображающая точка движется в направлении увеличения координаты х, поскольку при dt>G получаем dx>0, в нижней полуплоскости (г/<0) - в направлении уменьшения х, так как при dt>Q dx<Q.

Среди многочисленных фазовых траекторий особое значение имеют те, которые определяют возможные состояния равновесия и режимы периодических колебаний. Уравнение (4.191) однозначно определяет касательную к фазовой траектории во всех,точках, кроме тех, в которых одновременно

Р{хо, Уо)=0 и Q(Xo, уо) =0. (4.195)

Точки {хо, Уо), в которых выполняются условия (4.195), называются особыми точками. Фазовая скорость в особых точках равна нулю, поскольку производные dx/dt-О и dyldt=0, и поэтому координаты изображающей точки во времени не меняются: л;= =A;o=const и i/=yo=const. Следовательно, особые точки фазовой плоскости соответствуют состояниям равновесия системы.

Рассмотрим ряд примеров.

Пример 1. Свободные колебания в iC-контуре без потерь описываются уравнением

-+ = 0.

Решение этого уравнения х=А sin(№o/+(p) соответствует гармоническому колебанию, амплитуда А и фаза кр которого определяются начальными условиями. Покажем, что метод фазовой плоскости приводит к тому же результату. Согласно (4.187) записываем исходное уравнение второго порядка в виде друх зфавнений первого порядка:

dx dy

- (йах.

14.196)

Поделив почленно второе из этих уравнений на первое, получаем дифференциальное уравнение фазовых траекторий

dx у

Разделяя переменные и интегрируя, получаем уравнение фазовых траекторий

2 2ш2 ~ 14.i9ti

где С - постоянная интегрирования, определяемая начальными условиями. Фазовые граектории, соответствующие различным значениям С, имеют характер вложенных друг в друга эллипсов (рис. 4.35а).

Фазовая скорость г)ф= Уу+тх, подсчитанная согласно (4.190) и (4.196), ни в одной точке эллиптических траекторий не обращается в нуль. Поэтому последние соответствуют периодическим колебаниям.

Единственной особой точкой (1)ф=0) является начало координат (хо=0, уо=0). Особая точка, охваченная фазовыми траекториями, имеющими характер вложенных друг в друга замкнутых кривых (эллипсов, окружностей и пр.), называется особой точкой типа центра. Такая особая точка характеризуется тем, что в случае возникновения небольшого отклонения от состояния равновесия в системе возникают небольшие ненарастающие колебания около этого состояния. Изменением масштаба по одной из осей можно превратить фазовые траектории в круговые. Для этого достаточно заменить х иа A;i = a)oX- Подставляя x=Xil(i)o в (4.197), убеждаемся в том, что

При замене х на Xi фазовые траектории для различных С превращаются в концентри-ческие окружности (рнс. 4.356) радиуса р= ЧйсйоС. При движении по такой траектории фазовая скорость

иф== у {dxildt)+{dyldt)2= Y<i>oy4-(uoxh=mop

оказывается постоянной во всех точках, а угловая скорость перемещения юо-Сражающей точки по любой фазовой траектории to=tOo одна и та же. Это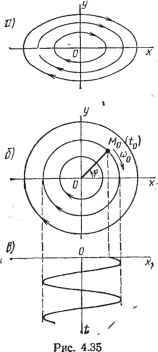

означает, что при любых отклонениях от состояния равновесия в системе возникают гармонические колебания Xi(i), определяемые проещией изображающей точки на ось абсцисс, амплитуда и фаза которых определяются начальными условиями (рис. 4.35е).

Пример 2. Колебания в колебательном контуре с потерями описываются уравнением

-г + 1 + = = 0> (4.198)

где ai=2a=rlL, й2=0)о=1/С. Переходные процессы в таком контуре имеют колебательный характер, если корки характеристического уравнения

Pi .2 = ~ Y ± / {-j ~ ° -

комплексные, т. е. c2>(ai/2)2. В последующем для упрощения выкладок считаем

a<S:(u\. (4.200)

Решение (4.198) при условии (4.200) имеет вид

х=Ае-а* 3m{mt+(f), (4.201)

где /4 и ф определяются начальными условиями, а частота свободных колебаний ©1 = Т/ио-а.

Для определения характера фазовых траекторий воспользуемся решением (4.201). Дифференцируя его, получаем

cos (©1 / + ф)--- Sin (©11 + (f)

На основании (4.200) пренебрегаем вторым слагаемым в квадратных скобках, принимая

у=Аа,1 е-о со5(ю1;+ф). (4,202) Заменяя х на Xi=(i)iX, имеем

х:1=Ла)1е-а(8т(ю1<+ф). (4.203)

Для построения фазовых траекторий на плоскости Xi,y обозначим

С01+ф=.ф, иИе-а = р (4.204)

и перепишем (4.203) и (4.202) в полярных координатах: .ti=psinil7, {/=pcos г!;.

Исключая из (4.204) время t, получаем уравнение фазовой траектории

р = ©1 Л е , (4.205)

соответствующее свертывающейся логарифмической спирали (рис. 4.36а). При иных начальных условиях получим другие спирали, сходящиеся к началу координат. Каждая спираль соответствует затухающему колебанию, построенному на рис. 4.36а. Начало координат соответствует устойчивой особой точке, ибо всякое отклонение от нее с течением времени затухает. Особая точка, охваченная фазовыми траекториями вида вложенных друг в друга закручивающихся спиралей, называется особой точкой типа устойчивого фокуса.

Если в (4.198) ai=2a<0 (отрицательное затзгхаиие может быть следствием использования положительной обратной связи или введения отрицательного сопротивления), величина р в (4.205) с течением времени будет возрастать, а потому фазовые траектории будут иметь характер раскручивающихся спиралей (рис. 4.366). Амплитуда таких колебаний будет нарастать по экспоненциальному закону, состояние равновесия окажется неустойчивым. Особые точки, охваченные фазовыми траекториями, имеющими характер вложен-