иых друг в друга раскручивающихся спиралей, называются особыми точками типа неустойчивого фокуса.

Пример 3. Процессы в контуре, описываемые (4.198), имеют апериодический хараетер. Корни характеристического уравнения (4.199) в этих условиях должны быть вещественными. Здесь возможны три случая: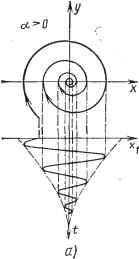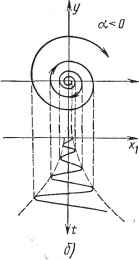

Рис. 4.36

1) а<0, ai -любое; корни и рг - действительные разных знаков: = 1 е + еР

(4.206)

Если iO и А2ФО, то с увеличением / одна компонента выражений (4.206) стремится к нулю, вторая - к бесконечности. Следовательно, с течением времени система удаляется от состояния равновесия; последнее оказывается неустойчивым. Хараетер получающихся фазовых траекторий вблизи особой точки х:о=0, о=0 показаны на рис. 4.37а. Такая особая точка называется седлом.

2) Й1>0, 0<a2<(ai/2)2; корни pi и Рз - действительные отрицательные. Величины каждого слагаемого в выражениях (4.206) стремятся к нулю. Лю-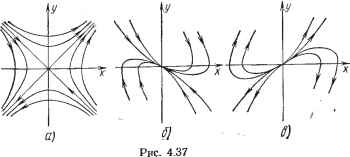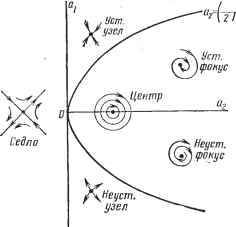

Рнс. 4.38

дл бая изображающая точка с течением времени приближается к особой точке пО апериодическому закону, как показано на рис. 4.376, особая точка устойчива Такая точка называется устойчивым узлом;

3) ai<0, 0<а2<(ai/2)2; корни Pi и рз - действительные положительные. Оба слагаемых в выражениях (4.206) нарастают, в результате чего изображающая точка удаляется от состояния равновесия по апериодическому закону, как показано иа рис. 4.37е. Особая точка неустойчива и называется неустойчивым узлом.

Зависимость хараетера особых точек от коэффициентов линейного уравнения (4.198) показана иа рис. 4.38.

Рассмотренные примеры показывают, что вид фазовых траекторий вблизи особой точки полностью определяет ее устойчивость. В частности, если изображающая точка с течением времени удаляется от состояния равновесия, последнее является неустойчивым, если приближается к нему, то асимптотически устойчивым.

В случае нелинейных систем исследование характера фазовых траекторий вблизи особых точек совпадает с исследованием устойчивости состояний равновесия по Ляпунову (см. § 4.2), при котором нелинейная система второго порядка (4.69) для малых отклонений заменяется линейной (4.74). Поскольку (4.74) не отличается от рассмотренного здесь уравнения (4.198), особые точки для нелинейных цепей второго порядка могут быть только тех же шести видов: центр, устойчивый и неустойчивый фокус, устойчивый и неустойчивый узел и седло.

Фазовые траектории бывают разомкнутые и замкнутые. Последние заслуживают особого внимания. Если изображающая точка движется по замкнутой фазовой траектории и притом такой, что ни в одной ее точке Пф не обращается в нуль, т. е. она не проходит через особую точку, то по прошествии некоторого определенного времени Т процесс (изменение л; и г/ во времени) будет повторяться. Следовательно, такая фазовая траектория характеризует периодическое колебание с периодом Т.

Замкнутые фазовые траектории, соответствующие возможным периодическим колебаниям, называются предельными циклами. Если соседние фазовые траектории с течением времени приближаются к предельному циклу, как показано ниже на рис. 4.39а, такой предельный цикл называется устойчивым; он соответствует устойчивому периодическому колебанию. Предельный цикл, от которого соседние фазовые траектории с течением времени удаляются, называется неустойчивым предельным циклом; он соответству-

ет неустойчивому периодическому режиму. В реальных системах могут существовать периодические колебания, соответствующие только устойчивым предельным циклам.

ФАЗОВЫЕ ПОРТРЕТЫ КОЛЕБАНИИ ГЕНЕРАТОРОВ

Фазовыми портретами колебаний исследуемых систем называют совокупность большого числа фазовых траекторий, определяющих характер процессов в системе при любых начальных условиях. Построим такие портреты для генераторов, работающих в различных режимах.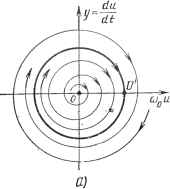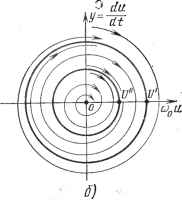

Рис. 4.39

На рис. 4.39а изображен фазовый портрет колебаний генератора в мягком режиме, соответствующем взаимоиндукции М=Мз на рис. 4.26, при которой в генераторе возможны два стационарных состояния: равновесия (точка 0) и периодических колебаний (точка Лз). Уравнение генератора (4.151) для этого режима ((х.э<: <0, 7>0) запишем как

du/dt=у, dy/dt= - [ (2аэ -1- v ) У+ o ] Фазовая скорость

vVy + [{2as+yu)y+aouy. (4.207J

Координаты щ, Уо особых точек (состояний равновесия) определяем из условия Vф=0. В правой части (4.207) оба подкоренных слагаемых положительны, поэтому Uo=0 и уо==0, единственная особая точка соответствует началу координат. При малых и (4.151) не отличается от (4.198), а поскольку аэ<0, особая точка имеет характер неустойчивого фокуса, т. е. фазовые траектории около нее соответствуют рис. 4.366.

Устойчивые периодические колебания с амплитудой U характеризуются устойчивым предельным циклом, который при надлежащем выборе масштабов близок по форме к окружности. Учиты-