ключе - конденсатор Са, при замкнутом - комбинация конденсаторов Сэ и Сд . Поэтому вектор состояния содержит лишь один элемент, дифференциальное-уравнение состояния при любом положении ключа оказывается первого порядка и его формирование нетрудно осуществить вручную (без помощи ЭВМ). Выберем в качестве переменной вектора состояния заряд

где 92;~Сд+9сэ-сумма зарядов соответствующих конденсаторов.

Используя эту переменную, уравнение состояния умножителя, как оказывается, можно записать так:

dxldtfpi(xy+hsm.(i)t+{Ee-E)/Rr<npwx0 ] dxldt=fp2(x)i+hsm&t+iE6-E)IRrnpwx<:0, ] *

где 4>i{x) и \(ра{х) -некоторые функции переменной состояния, определяемые-

свойствами транзистора. Два последних слагаемых в уравнениях (7.40) можно-.

трактовать как токи воздействия, т. е. компоненту Хвозд(0 в (7-2). Тогда функ--

ция f в (7.3) приобретает форму

ШШ X (П [ФМ+-*п *+(б-£)/г прихО, f (х(0, хвозд(0. t)- [ sinat+iE,-E)IR. при ;.<0.

Теперь обратимся к (7.4). Ток 4 приблизительно пропорционален q , чтое-

позволяет записать

(к = 9Сд/Тт=х/Тт {xG; при л:0 л:=9сд), (7.42)./

где Тт - некоторый параметр транзистора. Рассматривая в качестве выходной величины г/=.(к, г!.апишем

y{t)=B[x(t)]=-x{t), x{t)<0. (7.43%

Итак, (7.41) и (7.43) представляют уравнения (7.3) и (7.4) для рассматриваемой задачи Поскольку нас интересует не y(t), а только одна ее гармоника, нужно к операции определения добавить спектральный анализ последней .

Обратимся теперь к априорной информации о цепи. Будем считать, что в-данной неавтономной цепи устанавливается единственный периодический режим с известным периодом 2я/ю.

В данном ключевой схеме в любом положении ключа имеется один реактивный элемент, определяющий постоянную времени, которая может быть найдена по функциям <р1(л;) и ф2(л:). Последние могут быть представлены как

(i>i{x)=xli{x), (f2(.x)=xlxa(x). С7.44>

где Тр и Тэ-некоторые постоянные времени, зависящие от координаты х. Если удается предвидеть область возможных изменений х, то, зная параметры, конкретного транзистора, можно выбрать некоторые средние в области изменения x значения т р и Тэ и принять их за постоянные времени цепн дл л;0 и х<0. Так, для транзистора КТ-912 можно принять Тр=Тэ=4-10- с-

(при определенном выборе Rr).

Переходим к определению динамического режима умножителя и его характеристик. Задача сводится к расчету зависимостей {к(1) и последующему нахождению амплитуды и фазы определенной составляющей тока 1к. Чтобы най- ти (к(0. необходимо проинтегрировать на ЭВМ уравнения (7.40) и затем воспользоваться (7.42). Поскольку проблема постоянных времени в данной задаче не возникает, можно избрать явный метод интегрирования, например явный метод Эйлера, при достаточно малом шаге. Для оценки момента наступления-стационарного режима изберем критерий (7.36) при 62= 0,0001. Обращаться к

Это связано с тем, что в уравнениях состояния не учтен контур LC умножителя. Достигаемое при этом упрощение уравнений столь существенно, чтс-оправдывает необходимость усложнения процесса обработки y(t) при вычислениях на ЭВМ.

специальным методам ускорения расчета стационарного режима нет необходимости, так как этот режим достигается всего через несколько интервалов, равных периоду 2я/ш. Для подсчета коэффициентов Фурье функции / (О при малых номерах гармоник можно использовать общие методы вычисления интегралов, известные из курса вычислительной математики.

Итак, умножитель рассчитывается на ЭВМ в следующем порядке: I) вводим в ЭВМ уравнения (7.40) и константу из (7.42); задаем номер интересующей гармоники; 2) вводим начальное условие Хо, например л;(0)=-0,1; 3) пользуясь алгоритмом явного метода Эйлера, интегрируем второе уравнение (7.40), проверяя на каждом шаге условие х<0; 4) как только стало хО, переходим к первому уравнению (7.40); продолжаем интегрирование, пока не стало х<0, . и т. д. 5) подобный расчет продолжается в течение двух интервалов оси t, каждый длиной 2п/а>; по окончании расчета на интервале / от О до 4я/и производится проверка условия (7.36), причем интеграл в левой части неравенства вычисляется по одной из формул численного интегрирования (например, методом прямоугольников); если неравенство не выполнено, продолжаем расчет далее на интервале от in/a до бя/ю и вновь проверяем условие (7.36) и т. д. Как только условие стационарности будет выполнено, запоминаем массив неотрицательных значений x(i), отвечающих последнему рассчитанному

периоду x{t); 6) рассчитываем iK{t) по (7.42) для последнего периода и запоминаем массив к(0; 7) рассчитываем амплитуду и фазу нужной гармоники.

Соответствующие расчеты обычно повторяются для ряда значений входного воздействия Ibi и частоты ю, различных £6 и разных параметров тран-

зисторов и кратностей умножения. На

1 т рис. 7.5 представлены рассчитанные на ЭВМ Наири-2 зависимости амплитуды Аз (сплошные линии) и фазы фз (пунктир) третьей гармоники тока t(0 для ряда значений т=

= 1вх11в1тах И ВХОДНЫХ чаСТОТ

{1вхтах - максимальная амплитуда, принятая в расчетах), отвечающих низкочастотным (т), высокочастотным (юз) и среднечастотным (юг) умножителям (юз>1Ю2>.т1). Видно, что с увеличением частоты эффективность процесса умножения на данном транзисторе падает; фаза вькодного колебания зависит от частоты и амплитуды hx. Заметим, ЧТО получить эти результаты без применения ЭВМ было бы невозможно.

ПРИЛОЖЕНИЕ 1

ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ, ИСПОЛЬЗУЕМЫЕ ПРИ ГАРМОНИЧЕСКОМ АНАЛИЗЕ КОЛЕБАНИИ

1. cos а=(1-I-COS 2а) 2. cos= о,=- (3 cos a+cos За)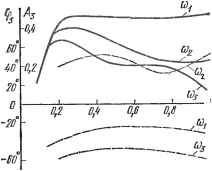

Рис. 7.5

3. cos а=~ (3-f4 cos 2a-f-oos 4а) 4. oos .а= -~ (lOcos а+5 cos 3a+cos ба)

5. cos а=(10+15 COS За+б cos 4a-+cos 6а)

6. cos а=- (05 cos a-f-ai cos 3ai+7 cos 5a-boos 7a) 7. sin a= - (1-cos 2a)

8. sins a= -r (3 sin a-sin 3a) 9. sin a= (3-4cos 2a-boos4a) 4 о

30. sin5 a=- (10 sin ot- sinStf+sin 5a) lb

11. cosasina=-sin2a 12. sinasraP=-[cos( -P)-cos(a+P)] 13. sin a DOS p=-[>ш(а+Р)+sin(a-iP)]

.14. COS a cos P=[cos (a-P) -f cos (a+P) ] :

ПРИЛОЖЕНИЕ 2

НЕКОТОРЫЕ МАТРИЧНО-ВЕКТОРНЫЕ СООТНОШЕНИЯ

Матрицей типа тХя называется таблица, составленная из вещественных или комплексных констант, функций времени и т. д., записываемая как

А= [ао1.

где первый индекс указывает на номер строки, второй - столбца.

Матрица типа mXi называется вектором-столбцом, а типа 1Хп-вектором-строкой. Соответственно имеем

Производная и интеграл от х(/) по времени определяются так:

dXm dt

Xi(t)dt

J xm (0 dt

T. e. они образованы производными и интегралами от компонент вектора.

Норма вектора ПхЦ может определяться по-разному, в частности, как: 11x11 = тал:(л;1, \хт\) или как llxi = V \xi\+ ... +\Хт\, причем в первом случае имеется в виду наибольший из всех модулей компонентов х.

С помощью матриц и векторов удобно и компактно записываются алгебраические и дифференциальные уравнения и различные соотношения, характеризующие нелинейные цепи. Например, зависимость у-го тока от совокупности напряжений щ, Un, записываемая в традиционной форме как i}=ij(uu ы ) может- быть сокращенно переписана в виде гз=1з(и), и совокупность всех токов i=i(u).

Система алгебраических или трансцендентных уравнений вида

/i( i, м )=0.

/п(Ы1, Un)=0.

в матрично-векторной форме выглядит таким образом: f(u) =

где f - вектор-столбец, составленный из компонент-функций f, fn. Система дифференциальных уравнений в нормальной форме Коши