использовать любой другой узел, ни одна из других проводимостей схемы при вычислении определителя также не умножается сама на себя

Таким образом, определитель (3-1) представляет собой сумму произведений троек проводимостей аЬс, bed и т. д. Эти произведения представляют собой определители простейших схем типа рис. 3-2 г, д, называемых деревьями. Всё шестнадцать деревьев схемы рис. 3-3 а, б изображены на рис. 3-4. Определитель этой схемы содержит сумму из шестнадцати соответствуюш,их произведений троек проводимостей.

Для топологической контурной схемы любой сложности дерево представляет собой совокупность соединенных ветвей, касающихся всех узлов, но не образующих ни одного замкнутого контура. Величина дерева - произведение проводимостей его ветвей. Для простоты понятия дерево и величина дерева можно отождествить.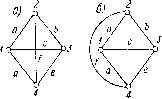

Рис. 3-3. По.чная топо,логичес-кая схема (а) и ее эквива .тент (б).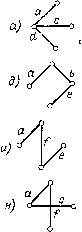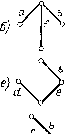

н) л)

о) °~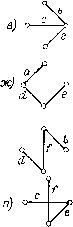

Рис. 3-4. Деревья схемы, изображенной па рис. 3-3.

Одна из важнейших формул топологического анализа сводится к тому, что определитель цепи равен сумме ее деревьев [12].

в этом можно убедиться и непосредствепны.ч вычис.чснием оиреде1 теля (3-1). Все слагаемые, содержащие проводимости в квадрате, сокращаются.

о 3.3. Топологические методы вычисления определителя электрической цепи

В случае сложных схем отыскание всех возможных деревьев педставляет собой достаточно трудоемкий процесс, требующий большого внимания, поскольку неучет хотя бы одного дерева ведет к ложному результату. Однако существует ряд методов разложения определителя на множители, упрощающих вычисления. Яля этого вводятся [12] дополнительные понятия пути и его алгебраического дополнения: путь - простая совокупность ветвей, присоединенных к двум заданным уалам, представляющая собой непрерывную последовательность ветвей, вдоль которой каждый изел встречается не более одного раза. Величина пути - произведение проводимостей ветвей пути k. Как и в случае дерева, понятия пути и величины пути можно отождествить. Алгебраическое дополнение пути - определитель цепи, остающейся после вычеркивания (короткого замыкания) всех ветвей пути k.

Рассмотрим метод разложения определителя на пути или по узловой паре. Выберем два любых узла схемы. Согласно определению все деревья проходят через эти узлы, вообще говоря, по разным путям между этими узлами. Однако путей, связывающих два узла, меньше, чем деревьев, так как один и тот же путь входит в группу деревьев. При этом величина пути является общим множителем для величин этой группы. После вынесения общего множителя величины пути за скобку в ней остается сумма всех возможных комбинаций всех ветвей, кроме входящих в путь, иными словами - сумма всех деревьев (т. е. определитель) цепи, у которой замкнуты ветви, соответствующие выбранному пути. Учитывая все пути между двумя выбранными узлами, мы охватим все деревья исходной цепи, т. е. найдем ее определитель. Математически это правило разложения определителя на множители записывается в виде

A = SPftAft. (3-2)

Иллюстрируем это правило на примере цепи рис. 3-3, а. Вымрем узловую пару 1-3. Ее соединяют пять путей аЬ, de, с, WH dfb. Первый из этих путей входит в три дерева abf, abe и wa, показанных соответственно на рис. 3-4, б, д, з. Вынося за скобку величину пути Р - аЬ, в скобке получим алгебраическое дополнение l\ = f еd. Топологически этот результат легко отлучается, если в схеме рис. 3-3, а замкнуть ветви а и Ь, т. е. оединить между собой узлы 1, 2 м 3. В результате ветви f, е рис oiy соединенными в параллель, и в соответствии с Нение определитель этого соединения (алгебраическое допол-способ равен сумме ветвей. Совершенно аналогичным

К=,аА- h 2 = с?е найдем алгебраическое дополнение

тЬ. Произведение PA равно сумме деревьев,

изображенных на рис. 3-4, г, е, ж. Путь Р-л = с входит в 8 деревьев (рис. 3-4, а, б, к, м, н, о, п, р). После замыкания этого пути схема рис. 3-3, а превращается в треугольник со сторонами (а щ \de)\if. Определитель такого треугольника представляет собой сумму его деревьев A3 = (а + Ь) (d + е) + {d + е) f-\-f {а-\~ b). Произведение Рз Аз дает сумму упомянутых восьми деревьев исходной цепи. Наконец, последние два пути Pafe и P = dfb представляют собой деревья рис. 3-4, и, л рассматриваемой схемы. После замыкания этих путей схема (рис. 3-3, а) превращается в одни узел, определитель которого (алгебраическое дополнение деревьев) согласно рис. 3-2, б, равен единице. Таким образом, разложение (3-2) представляет сумму всех шестнадцати деревьев схемы, чем подтверждается его справедливость.

В ряде случаев удобным оказывается метод разложения определителя по узлу . Все деревья схемы согласно определению проходят через любой выбранный узел или ограничиваются в этом узле, поэтому их можно разбить на группы, отличающиеся друг от друга тем, какие и сколько они содержат ветвей, выходяццгх из данного узла. Поясним этот метод на примере узла 2, связывающего три ветви а, b и f (рис. 3-3, а). Деревья, включающие только одну из этих ветвей а, соответствуют исходной схеме, если удалить из нее (разомкнуть) две другие ветви Ь я f. Поскольку ветвь а является общим множителем, т. е. входит в каждое из этих деревьев, их сумму можно записать в виде а Д, где Ад - определитель исходной схемы, в которой ветвь а замкнута, а ветви b nf разомкнуты (удалены). В данном случае (рис. 3-3, а) схема соответствует треугольнику со сторонами с, d я е, определитель которого, вычисляемый по сумме деревьев, равен Да,=

- cd-\-de-kec. Нетрудно убедиться, что деревья, содержащие только ветвь а, начинающуюся в узле 2, показанные на рис. 3-4, а, ж, м, действительно дают в сумме величину аАй =

- a{cd-\~de-\-ec).

Аналогично можно выделить группы деревьев бА, и fA, содержащие только ветвь b или только ветвь f, начинающуюся в узле 2. Определители А , А и А/ соответствуют одной и топ же схеме, в данном случае треугольнику с, d, е, поэтому они равны друг другу. Деревья, содержащие одновременно только ветви а п Ь, выходящие из узла 2, соответствуют исходной схеме после удаления в ней ветви /. Вынесение за скобку общего множителя аЬ соответствует замыканию этих ветвей (соединению узлов /, 2, 3). В данном примере схема рис. 3-3, а превращается в параллельное соединение ветвей end, определитель которого равен ab = e-\-d, поэтому сумма упомянутых деревьев равна аЬ 1\аь==оЬ{еd), в чем нетрудно убедиться путем непосредственного суммирования этих деревьев (рис. 3-4, д, з).

Аналогичным путем получим выражения af А и bfbf,

торых b.af и tbf соответствуют исходной схеме после замыкания

---------- - - - - ----------- ------ --- ~ I) й I

livi.---

в ней ветвей а и f и удаления ветви Ь, либо замыкания 108