Для иллюстрации некоторых определений и понятий [12] рас-мотрим приведенный на рис. 4-3, а граф более сложной цепи, описываемой системой четырех уравнений:

X4 = toiX(,~txiXx UiX; (4-1)

Xft = tiiXi /34X3.

Ветвь, у которой индексы расположены в порядке возрастания (оь -2. 14 и др.), называется прямой, в противном случае ветвь (/м) называется обратной. Узел (например, Xi, х, х, Xj), имеющий одну или несколько входящих ветвей, называется зависимым.

Путь - непрерывная последовательность ветвей, соответствующая их направлениям, проходящая через каждый узел не более одного раза (например, Uu tn, tn, tu и др.) Контур (обратной связи) - замкнутый путь (например, 23, /32 или 33).

Узел, т входящий ни в один контур обратной связи, называется каскадным [13]. К числу каскадных узлов относятся источники, содержащие только входящие ветви (например, х), стоки, содержащие только входящие ветви {xi) и простые каскадные узлы, содержащие как выходящие, так и входящие ветви (х). Следует заметить, что в качестве стока может фигурировать любой зависимый узел, поскольку добавлением единичной ветви можно преобразовать его сток (например, Хч в х, как показано пунктиром на рис. 4-3, а). Нередко такая операция подразумевается, но не показывается на графе.

Если граф не содержит ни одного явно выраженного источника (на рис. 4-3, а это имело бы место, если бы существовала ветвь /зо, показанная пунктиром), то в качестве источника можно выбрать любой зависимый узел, добавляя к нему (мысленно) ветвь единичной величины (например, х1х на рис. 4-3, а).

Граф, не содержащий контуров обратной связи, называется каскадным. В частности, устранение обратной ветви /32 и петли 33 (/з2 = зз = 0) графа рис. 4-3 превращает его в каскадный.

В результате составления и анализа, обычно требуется найти передачу графа Т, представляющую собой отношение сигнала заданного зависимого узла к сигналу источника. Таким образом, правильно составленный граф должен иметь лишь один узел-источник. Если в реальной схеме имеется несколько узлов-источников сигнала, необходимо для каждого из них надлежатцим образом рестроить граф и найти результат, воспользовавшись теоремой суперпозиции.

§ 4-2. Определение передачи графа

а-cj преобразования графов иллюстрированы рис. 4-4, текае тность схем, изображенных на рис. 4-4, а, вы-т из принципа суперпозиции: х[ = ахи xJ-bxi, Хч = х-\-

-xJ = {a-\ b)Xi. Рисунки 4-4, б-г иллюстрируют исключение переменных х., или Х;, из соответствующих уравпеиин.

Для рис. 4-4, б имеем x-axs, = отсюда х-==аЬх, Для рис. 4-4, в: х. -ахх-]- Ьх. х-г~-г-схз, Xi=acXi y-bcxl; рис. 4-4, г: х = ахи х = Ьх, х - сх, Хз-=аЬх1, Xi = acxi.

Граф рис. 4-4, д отображает уравнения х = ахх-\ Ьх Xi = axt/il -Ь) и х = сх.2, отсюда x.i = acxij{l Ь).

Очевидно, что аналогичные преобразования возможны и в том случае, когда больше двух ветвей суммируются (рис. 4-4, а), умножаются (рис. 4-4, б), входят в один узел (рис. 4-4, в) нлп выходят из одного узла (рис. 4-4, г). Последовательность июгнх ветвей типа рис. 4-4, б представляет собой путь. Передача эквивалентной ветви, т. е. передача пути Р равна произведению не-

Р= й:,о- -oxg редач величин ветвей вдоль

этого пути. Передача контура (замкнутого пути) L также рав-

хр--на произведению ветвей.

Пользуясь преобразованиями рис. 4-4, а-д, можно найти передачу графа. Для этого пе-хго-с лесообразно прежде всего исклю-

чить простые каскадные узлы i--- графа (например, узел Xi, на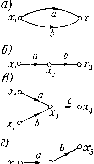

--.. Р- путем определения

х ас 0X4 передач всех путей между рас-

) ас сматриваемыми узлами (напри-

= л,о--oxs мер, 0112 И . между узлами

Хд и Xi) и суммирования их

Рис. 4-4. Эквивалентные преобразо- (рис. 4-3, б). Далее МОЖНО упрос-вания графов. тить сложные контуры обратной

связи, содержащие более одного узла, исключить некоторые узлы и превратить эти контуры в простые петли, включающие лишь по одному узлу. Например, на рис. 4-3,6 можно исключить узел х, добавляя к передаче / oi между узлами Хд и передачу пути от узла Хо через Xi к x-i, т.е. (0-2 4-4iia) 2з> а к петле с передачей fg, касающейся узла лгз, добавить передачу петли 3.223 (рис. 4-3, в).

В результате подобных упрощений остаются только узлы-источники, узлы-стоки и узлы, входящие в простые петли обратной связи. Минимальное число узлов последнего типа называется индексом графа, а сами узлы - узлами индекса (например, узел -з на рис. 4-3, в). После преобразований, в результате которых остаются только источники, стоки и узлы индекса, исходный 1 раф (рис. 4-3, а) превращается в подграф индекса (рис. 4-3, в). Сле дующим этапом является учет влияния простых петель обратгю связи и вычисление передачи графа. Учитывая преобразовани рис. 4-4, д, можно найти передачу вдоль пути с узлами -о - -

i учетом петли) и, сложив ее с непосредственной передачей ti t , определить результирующую передачу T,i от узла л , к узлу х

7 = 704. - 01 hi -г------j----т----у-.------ (4-Z)

Контур обратной связи, можно разорвать, расщепив необходимый узел на два, один из которых объединяет все выходящие ветви, т. е. является источником, а другой представляет собой сток,объединяющий все входящие ветви. Так, например, для разрыва контура 4з 4з (рис. 4-3, а) достаточно заменить x.j. узлом Х2 С выходящей ветвью 4з и узлом Х2 с входящими ветвями / с tn, t-ii, соединив образованные узлы {х и х2) единичной ветвью. Однако более эффективным является расщепление узла на узлы хз и Хз, поскольку при этом разрываются сразу два контура обратной связи 3223 и /33 (рис. 4-5, а, б).

В общем случае минимальное число узлов, которые необходимо расщепить, чтобы разорвать все контуры обратной связи, равно индексу графа, поскольку эти узлы можно выбрать в качестве узлов индекса, устранив остальные (кроме источников и стоков) в процессе преобразования графа в подграф индекса.

Общая формула для вычисления передачи графа от узла j к узлу k, предложенная Мэзоном [12], имеет вид:

li -.L,){\-L,). . .{Г-1)\

где Pi,P%, . Рп - передачи всех возможных путей от узла J к узлу k. Lx, Li, . . . Lm - передачи всех контуров, содержащихся в рассматриваемом графе. Звездочки в числителе и знаменателе означают, что при перемножении членов следует опустить такие произведения, которые содержат хотя бы один путь и контур или два контура, касающиеся друг друга (т. е. имеющие, по крайней мере, один общий узел).

Применяя формулу Мэзона к графу рис. 4-3, а или 4-5, а), найдем передачу от узла О к узлу 4. Существует четыре пути, свяшающих эти узлы: Pi = foi,4; l\, = t,it tc, Pt.inktu, fl* - 022334- Граф содержит два контура: Lj = t. tj- и L<i=ty. Контуры касаются друг друга, поэтому в выражении для знаменателя в (4-3) следует опустить произведение LiU:

[(l~ii) (1-12)]* = 1--1.2=1-3323-33.

Все пути, кроме Pi, касаются обоих контуров, поэтому числитель (4-3) имеет вид

{{Рх + Р2 + Рз + Р4) (1 - и) (1 - !,)]* = 1 (1 - -t - /-2) +

Подставляя сюда значения передач путей и контуров, не-РУдно убедиться, что, как н следовало ожидать, передача графа, численная по формуле (4-3), совпадает с ранее найденной (4-2).

б А. д. Артым \2%