-bbl±li. /4

При рассмотренном способе инверсии (рис. 4-5, а, б, в, г, д) узлы графа остаются неизменными, в то время как ряд ветвей изменяет свою величину. Однако можно применить другой способ инверсии, при котором ветви (кроме инвертируемой) сохраняют свою величину (но изменяют знак), а узлы не сохраняются, поскольку вводятся дополнительные единичные ветви и соответствующие узлы.

Сущность метода инверсии с сохранением ветвей поясним на примере того же графа (рис. 4-5, а).

Для инверсии ветви 4-2 запишем уравнение (4-4) в форме

.Го = (Х,2 tiiXi - tXt), (4-6)

что можно представить в виде двух уравнении

x, = Xi--tiiXi~-ta9X:i, (4-7)

х,= -х1 (4-8)

Это означает, что между узлами Хц и х инвертируемой ветви 2 необходимо ввести новый узел xi (узел х расщепляется на Х2 и хо). Из сравнения второго уравнения (4-1) и (4-7) видно, что этот узел имеет те же входящие ветви, что и х. (с обратными знаками), за исключением инвертируемой ветви t, которая заменяется единичной, начинающейся в узле Хо. Узел-источник Хо становится зависимым узлом, связанным согласно (4-8) с х ветвью 1До2, обратной инвертируемой (рис. 4-5, е).

Аналогичным способом, расщепив узел х , перенося все входящие в него ветви (с измененными знаками) к новому узлу х, связанному с х-е, единичной ветвью г33 = 1, а с Xg ветвью ta = ==1/4з, обратной инвертируемой 3, получим инверсию ветви (рис. 4-5, ж). Точно так же можно инвестировать ветвь tu (рис. 4-5, з).

Пользуясь формулой Мэзона (4-3), нетрудно убедиться, что передача инвертированного графа (оис. 4-5, з) не отличается от ранее найденной (4-5);

--h: }----

Г4 =-----

Анализируя рассмотренный процесс инверсии, можно сформулировать общее правило. Выбрав путь инверсии (02, 23, 34 на рис. 4-5, а), начинающийся из источника Хд или из любого зависимого узла, выбранного в качестве источника (если явный источник отсутствует), расщепляем каждый зависимый узел, лежащий на инвертируемом пути (узлы 2, х и Xj), и все входящие ветвп каждого из этих узлов с измененными знаками (-12, -t. - hi, -33. -hi) относим к полученным в результате расщеп! ления новым узлам {х, х и х1). Инверсный путь образуем, соединяя расщепленные узлы (х и хс, х и х, Xi и х1) единичными ветвями, а величины инвертируемых ветвей (42, 23, hi) заменяем на обратные -j-, ].

\ 02 23 34 /

Нетрудно заметить, что, если узел, лежащий на инвертируемом пути исходного графа {Xi на рис. 4-5, а), имеет только одну исходящую ветвь (/23), которая неизбежно инвертируется (поскольку только через нее может проходить инвертируемый путь), необходимость в расщеплении этого узла {х) в конечном счете отпадает, поскольку после инверсии (согласно рис. 4-5, ж, з) единственная входящая в него ветвь (I 23) от умножения на единичную выходящую не меняет своей величины. Эти две ветви могут быть заменены одной (пунктир на рис. 4-5, ж, з), т. е. можно объединить расщепленные узлы (xj и х).

§ 4-4, Анализ цепей, составленных из двухполюсников

Применяя закон Ома к каждой из р ветвей электрической цепи, получим р уравнений, которые определяют р неизвестных токов ветвей. Кроме того, для каждого из q узлов, в соответствии с первым законом Кирхгофа, можно составить уравнения равенства нулю суммы входящих и выходящих токов, из которых лишь q - 1 являются независимыми. Они определяют q-\ разностей потенциалов узлов относительно общего узла. Таким образом, общее число уравнений и соответственно неизвестных токов и напряжении ветвей равно p-Yq-l. Путем определенной Рис. 4-6. Мостовая схема, рационализации можно сократить число возбуждаемая генератором уравнений и неизвестных: в методе кон- турных токов оно равно р - ? + 1,

методе узловых напряжений - {q-ч-Граф цепи отображает систему уравнений, характеризующую цепь, поэтому при его составлении можно исходить как из токов и напряжений ветвей, так и из контурных токов или узловых напряжений. Зависимые узлы графа соответствуют неизвестным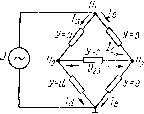

токам и напряжениям, а узлы-источники -внешним генераторам э д. с. и токов. Для иллюстрации применения метода графов для расчета пере-латочных функций цепей, составленных из двухполюсников, рассмотрим цепь, изображенную на рис. 4-6, где источником сигнала является генератор тока /, а нагрузкой - проводимость 7 = с, на которой необходимо определить падение напряжения

(/,з = (/.,-(/з = 1/,. (4-9)

В § 3-4 эта задача была решена топологическим методом с помощью контурной схемы (см. рис. 3-1, б), что дает возможность сравнить оба метода.

Цепь (рис. 4-6) описывается тремя независимыми уравнениями баланса токов в узлах и пятью уравнениями для разностей потенциалов ветвей. Эти уравнения записаны слева в приводимых ниже выражениях:

Данные уравнения позволяют найти восемь неизвестных напряжений и токов {Uu С/а, (/з, 1а, h, Ic, Ic), которыб выбираются в качестве зависимых узлов графа. Для каждого из этих узлов необходимо иметь уравнение, в котором соответствующие узлу ток или напряжение фигурировали бы в качестве функций Других токов и напряжений. Один из возможных отвечающих этому требованию вариантов записи уравнений представлен справа В выражениях (4-10) - (4-17), где источник / фигурирует только в Качестве аргумента, а каждая из неизвестных - только один раз в качестве функции. Эти уравнения совместно с (4-9) позволяют построить граф цепи. Для большей наглядности удобно

в VDa противном счучае появятся ложные источники, фигурирующие в лекк только как независимые переменные, например Uu С/ц, йенияг Риииях (4-10)-(4-17), и ложные стоки, фигурирующие в урав-Виях переменные, например i и в левых уравне-